Конвей, Джон Хортон: различия между версиями
| [отпатрулированная версия] | [отпатрулированная версия] |
отмена правки 106290331 участника 80.246.137.5 (обс.) Нет АИ Метка: отмена |
Категоризация |
||
| (не показано 109 промежуточных версий 38 участников) | |||
| Строка 1: | Строка 1: | ||
{{однофамильцы|Конуэй}} |
{{однофамильцы|Конуэй}} |
||
{{Учёный |
{{Учёный |
||
|Знаменитые ученики=- |
|||
| Дата рождения = 26.12.1937 |
|||
| Дата смерти = - |
|||
}} |
}} |
||
'''Джон Хо́ртон Ко́нвей''' ({{lang-en|John Horton Conway}}; |
'''Джон Хо́ртон Ко́нвей''' ({{lang-en|John Horton Conway}}; [[26 декабря]] [[1937 год|1937]] — [[11 апреля]] [[2020 год|2020]]) — британский [[математик]]. |
||
Известен в первую очередь как создатель [[Игра «Жизнь»|игры «Жизнь»]]. Однако его вклад в математику весьма многообразен и значителен. В [[Теория групп|теории групп]] он открыл [[группы Конвея]] и сформулировал [[Гипотеза чудовищного вздора|гипотезу чудовищного вздора]]. Совместно с соавторами заложил основы [[Комбинаторная теория игр|комбинаторной теории игр]], попутно открыв [[сюрреальные числа]]. Также внёс вклад в [[Теория узлов|теорию узлов]], [[Теория чисел|теорию чисел]]. Многие работы Конвея лежат в области [[Занимательная математика|занимательной математики]] или близки к ней. В целом он склонен исследовать красивые, наглядные объекты, такие как игры или [[многогранник]]и, не заботясь о том, какое значение это имеет с точки зрения фундаментальной или прикладной науки. |
Известен в первую очередь как создатель [[Игра «Жизнь»|игры «Жизнь»]]. Однако его вклад в математику весьма многообразен и значителен. В [[Теория групп|теории групп]] он открыл [[группы Конвея]] и сформулировал [[Гипотеза чудовищного вздора|гипотезу чудовищного вздора]]. Совместно с соавторами заложил основы [[Комбинаторная теория игр|комбинаторной теории игр]], попутно открыв [[сюрреальные числа]]. Также внёс вклад в [[Теория узлов|теорию узлов]], [[Теория чисел|теорию чисел]]. Многие работы Конвея лежат в области [[Занимательная математика|занимательной математики]] или близки к ней. В целом он был склонен исследовать красивые, наглядные объекты, такие как игры или [[многогранник]]и, не заботясь о том, какое значение это имеет с точки зрения фундаментальной или прикладной науки. |
||
Родился в [[Ливерпуль|Ливерпуле]]. Окончил [[Кембриджский университет]], получил там же степень [[Доктор философии|PhD]] в 1964 году и остался там же преподавать. На рубеже |
Родился в [[Ливерпуль|Ливерпуле]], Великобритания. Окончил [[Кембриджский университет]], получил там же степень [[Доктор философии|PhD]] в 1964 году и остался там же преподавать. На рубеже 1960—70-х годов стал известен как в профессиональном сообществе (благодаря группам Конвея), так и среди широкой публики (благодаря игре «Жизнь»). С 1986 года работал в [[Принстонский университет|Принстонском университете]], [[США]]. Был ярким лектором; помимо преподавания в университетах, читал лекции и писал статьи о математике для школьников и широкой публики. |
||
== Биография == |
== Биография == |
||
| Строка 19: | Строка 18: | ||
{{Внешние медиафайлы |
{{Внешние медиафайлы |
||
|image1 = [http://static.nautil.us/6534_5d44a2b0d85aa1a4dd3f218be6422c66.jpg Молодой Джон Конвей и его водяной компьютер WINNIE]<ref>{{cite web|title=This Early Computer Was Based on a Urinal Flush Mechanism |url= |
|image1 = [http://static.nautil.us/6534_5d44a2b0d85aa1a4dd3f218be6422c66.jpg Молодой Джон Конвей и его водяной компьютер WINNIE]<ref>{{cite web |title= This Early Computer Was Based on a Urinal Flush Mechanism |url= https://nautil.us/this-early-computer-was-based-on-a-urinal-flush-mechanism-235528/ |website= Nautilus |author= Siobhan Roberts |date= 2015-06-30 |accessdate= 2023-07-28 |archive-date= 2023-06-07 |archive-url= https://web.archive.org/web/20230607155244/https://nautil.us/this-early-computer-was-based-on-a-urinal-flush-mechanism-235528/ |deadlink= no }}</ref> |
||
}} |
}} |
||
В 1956 году поступил в [[колледж Гонвилл-энд-Киз]] [[Кембриджский университет|Кембриджского университета]], причём решил вести себя там как [[экстраверт]]<ref name="Roberts1" />. И действительно, в Кембридже он завёл друзей, вовлекался в разнообразную околоучебную и общественную деятельность. В частности, там он познакомился с Майклом Гаем, сыном математика [[Гай, Ричард Кеннет|Ричарда Гая]]; Майкл Гай стал лучшим другом Конвея и его соавтором по нескольким работам{{переход|Орбифолды, многогранники и замощения}}. Помимо прочего, в Кембридже Конвей с друзьями построили цифровой компьютер, работавший на водяных трубах и клапанах. Он проводил много времени за всевозможными играми и, в частности, играл с [[Безикович, Абрам Самойлович|Абрамом Самойловичем Безиковичем]] в карточную игру «Свои козыри» в особой модификации Безиковича. Академическая успеваемость Конвея поначалу была на высоте, но затем ухудшилась<ref name="Roberts3" />. |
В 1956 году поступил в [[колледж Гонвилл-энд-Киз]] [[Кембриджский университет|Кембриджского университета]], причём решил вести себя там как [[экстраверт]]<ref name="Roberts1" />. И действительно, в Кембридже он завёл друзей, вовлекался в разнообразную околоучебную и общественную деятельность. В частности, там он познакомился с Майклом Гаем, сыном математика [[Гай, Ричард Кеннет|Ричарда Гая]]; Майкл Гай стал лучшим другом Конвея и его соавтором по нескольким работам{{переход|Орбифолды, многогранники и замощения}}. Помимо прочего, в Кембридже Конвей с друзьями построили цифровой компьютер, работавший на водяных трубах и клапанах. Он проводил много времени за всевозможными играми и, в частности, играл с [[Безикович, Абрам Самойлович|Абрамом Самойловичем Безиковичем]] в карточную игру «[[Свои козыри]]» в особой модификации Безиковича. Академическая успеваемость Конвея поначалу была на высоте, но затем ухудшилась<ref name="Roberts3" />. |
||
В 1961 году женился на Эйлин Фрэнсис Хау<ref name="Roberts3" />. У Эйлин образование в области иностранных языков: французский и итальянский<ref name="Roberts5" />. У Джона и Эйлин родились четыре дочери в 1962—1968 годах: Сьюзан, Роуз, Елена и Энн-Луиза<ref name="MacTutor" />. |
В 1961 году женился на Эйлин Фрэнсис Хау<ref name="Roberts3" />. У Эйлин образование в области иностранных языков: французский и итальянский<ref name="Roberts5" />. У Джона и Эйлин родились четыре дочери в 1962—1968 годах: Сьюзан, Роуз, Елена и Энн-Луиза<ref name="MacTutor" />. |
||
| Строка 32: | Строка 31: | ||
[[Файл:Sprouts-2spot-game.png|right|300px|thumb|Короткая партия в рассаду: своим ходом каждый игрок соединяет две точки линией и ставит на ней новую точку, из точки исходит не более трёх линий; кто не может сделать ход — проигрывает.]] |
[[Файл:Sprouts-2spot-game.png|right|300px|thumb|Короткая партия в рассаду: своим ходом каждый игрок соединяет две точки линией и ставит на ней новую точку, из точки исходит не более трёх линий; кто не может сделать ход — проигрывает.]] |
||
{{Внешние медиафайлы |
|||
| ⚫ | Конвей много играл в математические игры с коллегами и студентами и регулярно придумывал их. Так, со студентом Майклом Патерсоном они изобрели топологическую игру [[Рассада (игра)|рассада]], которая немедленно приобрела на кафедре тотальную популярность. Конвей стал переписываться с [[Гарднер, Мартин|Мартином Гарднером]]: об играх, включая рассаду, а также об алгоритме для решения разновидности [[Справедливый делёж|задачи о справедливом дележе]] (открытом им независимо от более раннего решения Джона Селфриджа<ref name="bramstaylor116">{{публикация|книга | isbn = 0521556449 | заглавие = Fair Division. From cake-cutting to dispute resolution | автор = Steven J. Brams and Alan D. Taylor | издательство = Cambridge University Press | год = 1996 | pages = 116 }}</ref>). Кроме того, Конвей пытался визуально представить [[четырёхмерное пространство]], и для этого он тренировал [[бинокулярное зрение]] с вертикальным [[параллакс]]ом вместо горизонтального с помощью специального устройства. В этот же период он с коллегами исследовал [[последовательность «Посмотри-и-скажи»]]; как нередко |
||
|width = 310px |
|||
|image1 = [https://thestar.com/content/tncms/assets/v3/editorial/3/ec/3eca99a9-f6b4-517d-a378-9049702ba800/63ea9aab4978a.image.jpg Джон и Эйлин с дочерьми] в конце 1960-х<ref>{{cite web |title= Inside the mind of ‘mathemagician’ John Horton Conway |url= https://www.thestar.com/news/insight/inside-the-mind-of-mathemagician-john-horton-conway/article_38b7bcd9-779c-58f8-ac12-d8e5ec61cea2.html |website= The Toronto Star |author= Siobhan Roberts |date= 2015-08-23 |accessdate= 2023-09-12 |archive-date= 2023-09-12 |archive-url= https://web.archive.org/web/20230912151934/https://www.thestar.com/news/insight/inside-the-mind-of-mathemagician-john-horton-conway/article_38b7bcd9-779c-58f8-ac12-d8e5ec61cea2.html |deadlink= no }}</ref> |
|||
|image2 = [https://www.52-insights.com/wp-content/uploads/2016/01/JHC-circa-1969-courtesy-of-John-Conway.jpg Джон Конвей] около 1969 г.<ref>{{cite web |title= John Conway. Genius Behind The Numbers |url= https://www.52-insights.com/john-conway-genius-behind-the-numbers/ |website= 52 Insights |author= Siobhan Roberts, John Horton Conway |date= 2016-01-07 |accessdate= 2023-03-11 |archive-date= 2023-03-11 |archive-url= https://web.archive.org/web/20230311144520/https://www.52-insights.com/john-conway-genius-behind-the-numbers/ |deadlink= no }}</ref> |
|||
}} |
|||
| ⚫ | Конвей много играл в математические игры с коллегами и студентами и регулярно придумывал их. Так, со студентом Майклом Патерсоном они изобрели топологическую игру [[Рассада (игра)|рассада]], которая немедленно приобрела на кафедре тотальную популярность. Конвей стал переписываться с [[Гарднер, Мартин|Мартином Гарднером]]: об играх, включая рассаду, а также об алгоритме для решения разновидности [[Справедливый делёж|задачи о справедливом дележе]] (открытом им независимо от более раннего решения Джона Селфриджа<ref name="bramstaylor116">{{публикация|книга | isbn = 0521556449 | заглавие = Fair Division. From cake-cutting to dispute resolution | автор = Steven J. Brams and Alan D. Taylor | издательство = Cambridge University Press | год = 1996 | pages = 116 }}</ref>). Кроме того, Конвей пытался визуально представить [[четырёхмерное пространство]], и для этого он тренировал [[бинокулярное зрение]] с вертикальным [[параллакс]]ом вместо горизонтального с помощью специального устройства. В этот же период он с коллегами исследовал [[последовательность «Посмотри-и-скажи»]]; как нередко случалось с его результатами, некоторые доказательства были неоднократно утеряны, найдены заново и в итоге опубликованы гораздо позже<ref name="Roberts5" />. |
||
В целом в период после защиты диссертации жизнь Конвея шла приятно и беззаботно. Но он не занимался «серьёзной» математической работой, и это его угнетало<ref name="Roberts5" />. |
В целом в период после защиты диссертации жизнь Конвея шла приятно и беззаботно. Но он не занимался «серьёзной» математической работой, и это его угнетало<ref name="Roberts5" />. |
||
=== Приход славы === |
=== Приход славы === |
||
Конец 1960-х и 1970-й годы выдались исключительно продуктивными для Конвея (он |
Конец 1960-х и 1970-й годы выдались исключительно продуктивными для Конвея (он именовал этот период ''[[annus mirabilis]]''<ref name="Roberts10" />): он нашёл три новые [[Спорадическая группа|спорадические группы]], названные его именем, придумал правила [[Игра «Жизнь»|игры «Жизнь»]] и построил [[сюрреальные числа]]. |
||
==== Группы Конвея ==== |
==== Группы Конвея ==== |
||
| Строка 46: | Строка 50: | ||
==== Игра «Жизнь» ==== |
==== Игра «Жизнь» ==== |
||
{{Внешние медиафайлы |
{{Внешние медиафайлы |
||
|image1 = [https:// |
|image1 = [https://www.quantamagazine.org/wp-content/uploads/2015/08/Conway_SurveyOfLifeForms.jpg Обзор форм «Жизни» Конвея]<ref name="RobertsQuanta">{{cite web |title= A Life in Games |url= https://www.quantamagazine.org/john-conways-life-in-games-20150828/ |website= Quanta |author= Siobhan Roberts |date= 2015-08-28 |accessdate= 2019-03-09 |archive-date= 2019-04-19 |archive-url= https://web.archive.org/web/20190419153710/https://www.quantamagazine.org/john-conways-life-in-games-20150828 |deadlink= no }}</ref> |
||
|image2 = [https:// |
|image2 = [https://www.quantamagazine.org/wp-content/uploads/2015/08/ConwayGameOfLife_KelvinBrodie_SunNews.jpg Конвей и игра «Жизнь», 1974 год]<ref name="RobertsQuanta" /> |
||
}} |
}} |
||
Конвей интересовался темой клеточных автоматов и, в частности, [[Автомат фон Неймана|автоматом фон Неймана]] ещё с детства. Он поставил целью придумать как можно более простой клеточный автомат с нетривиальным, непредсказуемым поведением, надеясь, что в таком |
Конвей интересовался темой клеточных автоматов и, в частности, [[Автомат фон Неймана|автоматом фон Неймана]] ещё с детства. Он поставил целью придумать как можно более простой клеточный автомат с нетривиальным, непредсказуемым поведением, надеясь, что в таком случае он будет [[Полнота по Тьюрингу|тьюринг-полным]]. Команда энтузиастов (Конвей, его коллеги и студенты) занималась перебором бесчисленных вариаций правил в поисках подходящих. Их усилия были вознаграждены, когда они придумали то, что стало известно как игра «Жизнь»{{переход|Клеточные автоматы}}. Конвей изложил основные сведения об игре «Жизнь», которые удалось выяснить, в письме к Мартину Гарднеру 1970 года. Тот написал об игре «Жизнь» в своей колонке в журнале ''[[Scientific American]]'', и эта заметка стала самой популярной из всех, вышедших в этой колонке. Игра «Жизнь» получила тысячи поклонников по всей Америке и за её пределами, а её изобретатель приобрёл известность среди широкой публики{{sfn|Roberts|2015|loc=8. Criteria of Virtue|name=Roberts8}}. |
||
Вскоре Конвей доказал тьюринг-полноту игры «Жизнь» (доказательство не было опубликовано). После этого он практически потерял интерес к этой теме. Он недоволен тем, насколько игра «Жизнь» более известна, чем другие его работы, и не слишком |
Вскоре Конвей доказал тьюринг-полноту игры «Жизнь» (доказательство не было опубликовано). После этого он практически потерял интерес к этой теме. Он был недоволен тем, насколько игра «Жизнь» более известна, чем другие его работы, и не слишком любил о ней рассказывать — кроме как отдельным интересующимся детям{{sfn|Roberts|2015|loc=9. Character Assassination|name=Roberts9}}<ref name="ORourke">{{публикация|статья|автор=Joseph O’Rourke |заглавие=Book Review. Genius at Play: The Curious Mind of John Horton Conway by Siobhan Roberts |издание=The College Mathematics Journal |год=2015 |ref=O’Rourke |issue=4 |volume=46 |pages=309—314 |doi=10.4169/college.math.j.46.4.309}}</ref>. |
||
==== Сюрреальные числа и книги об играх ==== |
==== Сюрреальные числа и книги об играх ==== |
||
Годы изобретения и обдумывания игр не прошли даром. Ричард Гай развил теорию, описывающую широкий класс игр, и когда во второй половине 1960-х годов он и американский математик [[Берлекэмп, Элвин|Элвин Берлекэмп]] задумали книгу об играх, они пригласили Конвея стать их соавтором<ref>{{публикация|книга|автор=Donald J. Albers, Gerald L. Alexanderson, eds.|заглавие=Fascinating Mathematical People: Interviews and Memoirs|издательство=Princeton University Press|год=2011|isbn=9781400839551|pages=175}}</ref>. Пока шла работа над книгой, получившей название ''Winning Ways for Your Mathematical Plays'', Конвей продолжал исследовать игры и обнаружил, что позиции в так называемых пристрастных играх могут быть выражены числами, причём |
Годы изобретения и обдумывания игр не прошли даром. Ричард Гай развил теорию, описывающую широкий класс игр, и когда во второй половине 1960-х годов он и американский математик [[Берлекэмп, Элвин|Элвин Берлекэмп]] задумали книгу об играх, они пригласили Конвея стать их соавтором<ref>{{публикация|книга|автор=Donald J. Albers, Gerald L. Alexanderson, eds.|заглавие=Fascinating Mathematical People: Interviews and Memoirs|издательство=Princeton University Press|год=2011|isbn=9781400839551|pages=175}}</ref>. Пока шла работа над книгой, получившей название ''Winning Ways for Your Mathematical Plays'', Конвей продолжал исследовать игры и обнаружил, что позиции в так называемых пристрастных играх могут быть выражены числами, причём класс необходимых для этого чисел включает не только [[Целые числа|целые]] и [[действительные числа]], но и некоторые новые числа{{переход|Комбинаторная теория игр}}. [[Дональд Кнут]] назвал эти числа сюрреальными. Конвей считал сюрреальные числа своим главным поводом для гордости{{sfn|Roberts|2015|loc=10. Snip, Clip, Prune, Lop|name=Roberts10}}{{sfn|Siegel|2013|loc=A Finite Loopfree History|name=Siegel}}. |
||
Хотя теория пристрастных игр вошла в ''Winning Ways'', она получила там не очень подробное освещение, особенно в части, касающейся сюрреальных чисел. Об этих числах Конвей написал Гарднеру в том же письме 1970 года, в котором сообщил об игре «Жизнь», а позже, в 1976 году, он быстро написал и выпустил собственную книгу ''On Numbers and Games'' о пристрастных играх и сюрреальных числах. Когда он сообщил об этом Берлекэмпу, тот был крайне недоволен и едва не рассорился с кембриджским соавтором, и только Гай смог помирить их. ''Winning Ways'' в итоге была дописана только в 1981 году; на следующий год книга вышла и стала бестселлером (несмотря на отсутствие рекламы от издательства), так же как и ''On Numbers and Games'' до того<ref name="Roberts10" /><ref name="Siegel" />. |
Хотя теория пристрастных игр вошла в ''Winning Ways'', она получила там не очень подробное освещение, особенно в части, касающейся сюрреальных чисел. Об этих числах Конвей написал Гарднеру в том же письме 1970 года, в котором сообщил об игре «Жизнь», а позже, в 1976 году, он быстро написал и выпустил собственную книгу ''On Numbers and Games'' о пристрастных играх и сюрреальных числах. Когда он сообщил об этом Берлекэмпу, тот был крайне недоволен и едва не рассорился с кембриджским соавтором, и только Гай смог помирить их. ''Winning Ways'' в итоге была дописана только в 1981 году; на следующий год книга вышла и стала бестселлером (несмотря на отсутствие рекламы от издательства), так же как и ''On Numbers and Games'' до того<ref name="Roberts10" /><ref name="Siegel" />. |
||
Эти две книги об играх, как и многие другие работы Конвея, несут явственный отпечаток его любви к неортодоксальной терминологии и [[каламбур]]ам<ref name="Roberts10" />: так, например, числа с чётным и нечётным количеством единиц в [[Двоичная система счисления|двоичной записи]] именуются, соответственно, [[Злое число|злыми]] и [[Одиозное число|одиозными]] — {{lang-en|evil}} и ''odious'', ср. с ''even'' и ''odd'' ({{tr-en|чётные}} и «нечётные»)<ref>{{публикация|статья |автор= J.-P. Allouche, Benoit Cloitre and V. Shevelev |заглавие= Beyond odious and evil |издание= Aequationes Mathematicae |volume=90 |pages=341—353 |год=2016 |doi= 10.1007/s00010-015-0345-3 | |
Эти две книги об играх, как и многие другие работы Конвея, несут явственный отпечаток его любви к неортодоксальной терминологии и [[каламбур]]ам<ref name="Roberts10" />: так, например, числа с чётным и нечётным количеством единиц в [[Двоичная система счисления|двоичной записи]] именуются, соответственно, [[Злое число|злыми]] и [[Одиозное число|одиозными]] — {{lang-en|evil}} и ''odious'', ср. с ''even'' и ''odd'' ({{tr-en|чётные}} и «нечётные»)<ref>{{публикация |1= статья |автор= J.-P. Allouche, Benoit Cloitre and V. Shevelev |заглавие= Beyond odious and evil |издание= Aequationes Mathematicae |volume= 90 |pages= 341—353 |год= 2016 |doi= 10.1007/s00010-015-0345-3 | arxiv=1405.6214}}</ref>. |
||
=== Работа над Атласом === |
=== Работа над Атласом === |
||
{{Внешние медиафайлы |
{{Внешние медиафайлы |
||
|image1 = [https:// |
|image1 = [https://web.archive.org/web/20160104182453im_/http://a3.files.biography.com/image/upload/c_fit,cs_srgb,dpr_1.0,q_80,w_620/MTM1MDQ3ODAxODMzNzk0MTc5.jpg Конвей и его детище — Атлас]<ref name="RobertsBiography">{{cite web |title= 7 Facts About the Charming "God-Monster" Mathematical Iconoclast John Horton Conway |url= https://www.biography.com/news/john-horton-conway-biography-facts |website= Biography |author= Siobhan Roberts |date= 2015-12-13 |accessdate= 2019-03-16 |archiveurl= https://web.archive.org/web/20160104181926/http://www.biography.com/news/john-horton-conway-biography-facts |archivedate= 2016-01-04 |deadlink= yes }}</ref> |
||
|image2 = [https://www.biography.com/.image/c_limit%2Ccs_srgb%2Cq_auto:good%2Cw_1400/MTM1MDQ3ODAxODMzNzk0MTc5/john-horton-conway-the-atlas-2.jpg Конвей и его детище — Атлас]<ref name="RobertsBiography" /> |
|||
}} |
}} |
||
В начале 1970-х годов Джон Конвей задумал составить справочник по конечным группам. Эту будущую книгу назвали «Атласом конечных групп» — ''Atlas of the Finite Groups''. В проекте приняли участие аспиранты Конвея Роберт Кёртис, Саймон Нортон и Роберт Уилсон, а также Ричард Паркер. Они собрали и перепроверили множество данных по конечным группам и в итоге приняли решение включить в Атлас в первую очередь [[Таблица характеров|таблицы характеров]]. Работа растянулась на много лет<ref name="AtlasHistory" group="JHC">{{публикация|книга|автор=John H. Conway, Robert T. Curtis and Robert A. Wilson|заглавие=The Atlas of Finite Groups: Ten Years on|часть=A brief history of the Atlas|издательство=Cambridge University Press|год=1998|isbn=0521575877}}</ref>{{sfn|Roberts|2015|loc=11. Dotto & Company|name=Roberts11}}. |
В начале 1970-х годов Джон Конвей задумал составить справочник по конечным группам. Эту будущую книгу назвали «Атласом конечных групп» — ''Atlas of the Finite Groups''. В проекте приняли участие аспиранты Конвея Роберт Кёртис, Саймон Нортон и Роберт Уилсон, а также Ричард Паркер. Они собрали и перепроверили множество данных по конечным группам и в итоге приняли решение включить в Атлас в первую очередь [[Таблица характеров|таблицы характеров]]. Работа растянулась на много лет<ref name="AtlasHistory" group="JHC">{{публикация|книга|автор=John H. Conway, Robert T. Curtis and Robert A. Wilson|заглавие=The Atlas of Finite Groups: Ten Years on|часть=A brief history of the Atlas|издательство=Cambridge University Press|год=1998|isbn=0521575877}}</ref>{{sfn|Roberts|2015|loc=11. Dotto & Company|name=Roberts11}}. |
||
| Строка 72: | Строка 75: | ||
[[Файл:Conway jh larissa queen.jpg|thumb|300px|Джон Конвей и Лариса Куин]] |
[[Файл:Conway jh larissa queen.jpg|thumb|300px|Джон Конвей и Лариса Куин]] |
||
В конце 1970-х годов Конвей расстался с Эйлин и встретил Ларису Куин |
В конце 1970-х годов Конвей расстался с Эйлин и встретил Ларису Куин. Лариса приехала из [[Волгоград]]а ([[СССР]])<ref>{{публикация|книга|автор=Alexander Masters|заглавие=Simon: The Genius in My Basement|часть=32 Atlas|издательство=HarperCollins|год=2011|isbn=9780007445264}}</ref> и была его аспиранткой<ref name="Times-obituary" />, занималась исследованием гипотезы чудовищного вздора; она получила степень [[PhD]] в Кембридже в 1981 году<ref>{{cite web |title=Larissa Queen |url=https://www.genealogy.math.ndsu.nodak.edu/id.php?id=71590 |website=[[Mathematics Genealogy Project]] |accessdate=2020-04-14 |quote=Some Relations between Finite Groups, Lie Groups and Modular Functions |archive-date=2018-08-09 |archive-url=https://web.archive.org/web/20180809042431/https://www.genealogy.math.ndsu.nodak.edu/id.php?id=71590 |deadlink=no }}</ref>. Джон и Лариса поженились в 1983 году, когда у них родился сын Алекс (на кафедре его прозвали малым монстром в честь группы). В 1983 году Конвей получил должность полного профессора. В первой половине 1980-х годов аспирантом Конвея стал [[Ричард Борчердс]], который позже доказал гипотезу чудовищого вздора{{sfn|Roberts|2015|loc=12. Truth Beauty, Beauty Truth|name=Roberts12}}. |
||
Между тем в 1984 году Атлас наконец был завершён. Ещё год ушёл на подготовку его к печати. Его публикация стала долгожданным событием для работавших в области теории групп математиков по всему миру<ref name="Roberts12" /><ref name="AtlasHistory" group="JHC" />. |
Между тем в 1984 году Атлас наконец был завершён. Ещё год ушёл на подготовку его к печати. Его публикация стала долгожданным событием для работавших в области теории групп математиков по всему миру<ref name="Roberts12" /><ref name="AtlasHistory" group="JHC" />. |
||
=== Принстон === |
=== Принстон === |
||
1986—1987 учебный год Джон Конвей провёл в [[Принстонский университет|Принстонском университете]], временно занимая по приглашению тогдашнего главы кафедры математики [[Стейн, Элиас (математик)|Элиаса Стайна]] только что учреждённую<ref>{{cite web|title= |
1986—1987 учебный год Джон Конвей провёл в [[Принстонский университет|Принстонском университете]] ([[США]]), временно занимая по приглашению тогдашнего главы кафедры математики [[Стейн, Элиас (математик)|Элиаса Стайна]] только что учреждённую<ref>{{cite web |title=Professorships |url=https://dof.princeton.edu/about/endowed-professorships-preceptorships-fellowships/professorships#:~:text=John%20von%20Neumann%20Professorship |website=Princeton University |accessdate=2023-04-24 |archive-date=2023-04-05 |archive-url=https://web.archive.org/web/20230405005323/https://dof.princeton.edu/about/endowed-professorships-preceptorships-fellowships/professorships |deadlink=no }}</ref> позицию [[Именная профессура|Фоннеймановского профессора]] прикладной и вычислительной математики. Конвею было предложено остаться на этой должности на постоянной основе. Он сильно колебался, но в итоге мнение жены, бо́льшая зарплата, уход из Кембриджа многих коллег-математиков и общее желание перемен склонили его принять предложение<ref name="Roberts12" />. |
||
[[Файл:William Thurston.jpg|200px|left|мини|Уильям Тёрстон]] |
[[Файл:William Thurston.jpg|200px|left|мини|Уильям Тёрстон]] |
||
| Строка 83: | Строка 86: | ||
[[Файл:Neil Sloane.jpg|200px|мини|Нил Слоун]] |
[[Файл:Neil Sloane.jpg|200px|мини|Нил Слоун]] |
||
Время от времени Конвей, рассказывая на различных выступлениях о тех или иных интересных нерешённых задачах, предлагал денежные призы за их решение. Размер приза соответствовал предполагаемой сложности задачи, и обычно он был сравнительно небольшой. Конвей |
Время от времени Конвей, рассказывая на различных выступлениях о тех или иных интересных нерешённых задачах, предлагал денежные призы за их решение. Размер приза соответствовал предполагаемой сложности задачи, и обычно он был сравнительно небольшой. Конвей дружил с [[Слоун, Нил|Нилом Слоуном]], автором «[[Энциклопедия целочисленных последовательностей|Энциклопедии целочисленных последовательностей]]», и неудивительно, что многие из этих задач были связаны с целочисленными последовательностями. В 1988 году произошла история с последовательностью, которая теперь известна как [[Последовательность Хофштадтера#10000-долларовая последовательность Хофштадтера — Конвея|10000-долларовая последовательность Хофштадтера — Конвея]]. Конвей намеревался предложить 1000 долларов за доказательство определённого утверждения об асимптотическом поведении последовательности, но, оговорившись, назвал в 10 раз большую сумму — весьма существенную для своего бюджета; при этом задача оказалась легче, чем предполагалось, и уже через две недели статистик Колин Мэллоуз решил её (с несущественной ошибкой, как позже оказалось). Узнав об оговорке Конвея, Мэллоуз отказался обналичивать присланный им чек, Конвей же настаивал на принятии приза; договорились они в итоге на 1000 долларов<ref name="Roberts14" />. |
||
{{Внешние медиафайлы |
|||
| ⚫ | |||
|image1 = [https://static01.nyt.com/images/2020/05/19/science/18SCI-CONWAY2/merlin_171560415_3990fa1f-2b6a-4fff-8e35-97943e6515ce-superJumbo.jpg Конвей в своём кабинете в Принстоне] в 1993 году: книги, модели многогранников и горы хлама<ref>{{cite web |title= Travels With John Conway, in 258 Septillion Dimensions |url= https://www.nytimes.com/2020/05/16/science/john-conway-math.html |website= The New York Times |author= Siobhan Roberts |date= 2020-05-16 |accessdate= 2023-03-11 |archive-date= 2023-03-11 |archive-url= https://web.archive.org/web/20230311144515/https://www.nytimes.com/2020/05/16/science/john-conway-math.html |deadlink= no }}</ref> |
|||
| ⚫ | В 1988 году в семье Джона |
||
}} |
|||
| ⚫ | В 1988 году в семье Джона и Ларисы родился сын Оливер (впоследствии оба их сына стали заниматься точными науками, следуя по стопам родителей). В 1992 году они пережили тяжёлый развод. Следствием этого для Конвея стали финансовые трудности и недостаток общения с сыновьями. У него случился инфаркт, на следующий год — ещё один. На фоне этих проблем предпринял попытку [[Самоубийство|самоубийства]], устроив себе передозировку лекарств. Восстановиться после этого физически и психологически ему помогли друзья, в первую очередь Нил Слоун<ref name="Roberts14" />. |
||
| ⚫ | |||
Третья жена Конвея, Диана, вышла за него замуж в 2001 году (они мирно разошлись через несколько лет{{sfn|Roberts|2015|loc=17. Humpty Dumpty's Prerogative|name=Roberts17}}), тогда же у них родился сын Гарет<ref name="MacTutor" />. |
|||
Конвей и его третья жена, Диана Катсоуджордж<ref name="Times-obituary">{{cite web|title=John Horton Conway obituary|url=https://www.thetimes.co.uk/article/john-horton-conway-obituary-dmbb8b2tw|website=The Times|date=2020-04-29|accessdate=2020-05-05|archive-date=2020-04-29|archive-url=https://web.archive.org/web/20200429050336/https://www.thetimes.co.uk/article/john-horton-conway-obituary-dmbb8b2tw|deadlink=yes}}</ref>, впервые встретились в 1996 году; она тогда работала в университетском книжном магазине<ref name="obit" />. Они поженились в 2001 году (и мирно разошлись через несколько лет, впоследствии активно общались{{sfn|Roberts|2015|loc=17. Humpty Dumpty's Prerogative|name=Roberts17}}), тогда же у них родился сын Гарет<ref name="MacTutor" />. |
|||
Конвей регулярно |
Конвей регулярно читал публичные популярные лекции на разнообразные темы, связанные с математикой, и с 1998 года преподавал в математических лагерях для школьников, таких как Canada/USA Mathcamp<ref>{{cite web|title=Mathcampers in Action!|url=http://mathcamp.org/action-new.htm|website=Canada/USA Mathcamp|archiveurl=https://web.archive.org/web/20010203125600/http://mathcamp.org:80/action-new.htm|archivedate=2001-02-03|deadlink=yes}}</ref>{{sfn|Roberts|2015|loc=16. Take It As Axiomatic|name=Roberts16}}. |
||
{{Внешние медиафайлы |
{{Внешние медиафайлы |
||
|image1 = [https:// |
|image1 = [https://www.quantamagazine.org/wp-content/uploads/2015/08/Conway_1k.jpg Джон Хортон Конвей в 2009 году]<ref name="RobertsQuanta" /> |
||
|image2 = [https:// |
|image2 = [https://old.maa.org/sites/default/files/images/upload_library/46/0_Halmos_Photos/JohnHandJohnB1999.jpg Математики Джон Х. Конвей и Джон Б. Конвей]<ref>{{cite web |title= Who's That Mathematician? Paul R. Halmos Collection - Page 59 |url= https://old.maa.org/press/periodicals/convergence/whos-that-mathematician-paul-r-halmos-collection-page-59 |website= MAA |author= Janet Beery and Carol Mead |date= 2012 |accessdate= 2024-10-26 |archive-date= 2019-04-05 |archive-url= https://web.archive.org/web/20190405074213/https://www.maa.org/press/periodicals/convergence/whos-that-mathematician-paul-r-halmos-collection-page-59 |deadlink= no }}</ref> |
||
}} |
}} |
||
В 2004 году Конвей и канадский математик Саймон Кошен доказали так называемую теорему о свободе воли{{переход|Квантовая механика}}; ещё некоторое время заняла подготовка публикации, и затем в течение нескольких лет соавторы теоремы развивали свой результат и обсуждали его с сообществом<ref name="Roberts1" />. |
В 2004 году Конвей и канадский математик Саймон Кошен доказали так называемую теорему о свободе воли{{переход|Квантовая механика}}; ещё некоторое время заняла подготовка публикации, и затем в течение нескольких лет соавторы теоремы развивали свой результат и обсуждали его с сообществом<ref name="Roberts1" />. |
||
Конвей ушёл на должность эмерит-профессора в 2013 году<ref name="Princeton-dof" />. |
Конвей ушёл на должность [[эмерит]]-профессора в 2013 году<ref name="Princeton-dof" />. В первые годы после формальной отставки он продолжил работать едва ли не активнее, чем до неё — выступать на конференциях, выпускать новые работы, преподавать в математических лагерях для школьников<ref name="Roberts1" />{{sfn|Roberts|2015|loc=Epilogue|name=RobertsEpilogue}}. |
||
В 2018 году он пережил обширный [[инсульт]]<ref>{{cite web|author=Kevin Hartnett|title=John Conway Solved Mathematical Problems With His Bare Hands|url=https://www.quantamagazine.org/john-conway-solved-mathematical-problems-with-his-bare-hands-20200420/|website=Quanta Magazine|date=2020-04-20|accessdate=2020-04-20|archive-date=2020-04-20|archive-url=https://web.archive.org/web/20200420155853/https://www.quantamagazine.org/john-conway-solved-mathematical-problems-with-his-bare-hands-20200420/|deadlink=no}}</ref>. |
|||
Скончался в [[Нью-Брансуик (Нью-Джерси)|Нью-Брансуике]] 11 апреля 2020 года в возрасте 82 лет от осложнений на фоне коронавирусной инфекции [[COVID-19]]<ref name="obit">{{cite web|author=Catherine Zandonella|title=Mathematician John Horton Conway, a ‘magical genius’ known for inventing the ‘Game of Life,’ dies at age 82|url=https://www.princeton.edu/news/2020/04/14/mathematician-john-horton-conway-magical-genius-known-inventing-game-life-dies-age|website=Princeton University|date=2020-04-14|accessdate=2020-04-14|archive-date=2020-04-15|archive-url=https://web.archive.org/web/20200415002150/https://www.princeton.edu/news/2020/04/14/mathematician-john-horton-conway-magical-genius-known-inventing-game-life-dies-age|deadlink=no}}</ref>. |
|||
== Личность == |
== Личность == |
||
[[Файл:John Conway browses Genius at Play.jpg|right|200px|thumb|Конвей листает собственную биографию]] |
|||
По свидетельствам людей, знавших Конвея, он был харизматичным и дружелюбным, при этом обладал значительным самомнением, что сам охотно признавал{{sfn|Roberts|2015|loc=Prologue|name=RobertsPrologue}}. Рассказывая о себе, нередко противоречил своим и чужим словам<ref name="Roberts2" />. Бытовыми сторонами жизни он пренебрегал, исключительно небрежно относился к полученным письмам и другим документам<ref name="RobertsPrologue" />. Хотя в целом вёл себя расслабленно, в периоды исследования математической задачи он работал много, интенсивно и дотошно<ref name="Roberts10" />. Математика была единственным интересом Конвея, при этом математические аспекты он замечал везде — не только в играх, но и в, казалось бы, бытовых предметах<ref name="Roberts12" />. С юности проявлял пацифистские взгляды<ref name="Roberts3" />, подписывал разнообразные политические петиции<ref name="Roberts6" />, хотя и не участвовал в политике активно. Был любвеобилен, не соблюдал верность своим жёнам, что и становилось одной из важных причин, по которой они расставались с ним<ref name="Roberts10" />. Атеист{{sfn|Roberts|2015|loc=7. Religion|name=Roberts7}}. |
|||
== Научный вклад == |
== Научный вклад == |
||
Джон Хортон Конвей |
Джон Хортон Конвей говорил, что не проработал ни дня в своей жизни, а лишь всегда играл в игры<ref name="RobertsPrologue" />. |
||
=== [[Теория групп]] и близкие области === |
=== [[Теория групп]] и близкие области === |
||
Конвей склонен подходить к исследованиям математических объектов, в том числе групп, с геометрической точки зрения, визуально представляя себе связанные с ними симметрии{{sfn|Roberts|2015|loc=15. Lustration|name=Roberts15}}, и вообще очень |
Конвей был склонен подходить к исследованиям математических объектов, в том числе групп, с геометрической точки зрения, визуально представляя себе связанные с ними симметрии{{sfn|Roberts|2015|loc=15. Lustration|name=Roberts15}}, и вообще очень ценил наглядность и красоту математических теорий<ref name="Roberts12" />. Кроме того, он предпочитал необычные частные случаи общим. Эти особенности стиля и склонностей Конвея ярко проявились в его работах по теории групп<ref name="Roberts15" />. |
||
==== Спорадические группы ==== |
==== Спорадические группы ==== |
||
| Строка 113: | Строка 122: | ||
Одно из самых важных достижений Конвея — исследование [[Группа автоморфизмов|группы автоморфизмов]] [[Решётка Лича|решётки Лича]] Co<sub>0</sub>. Он нашёл, что эта группа имеет порядок {{nobr|8 315 553 613 086 720 000}} и включает три новые спорадические группы [[Группа Конвея Co1|Co<sub>1</sub>]], Co<sub>2</sub>, Co<sub>3</sub> (их простота была впервые показана Джоном Томпсоном; Co<sub>0</sub> включает и некоторые другие спорадические группы, открытые незадолго до того{{sfn|Ronan|2006|p=155}}): Co<sub>1</sub> — [[факторгруппа]] Co<sub>0</sub> по её [[Центр группы|центру]], единственным нетривиальным элементом которого является домножение на −1, Co<sub>2</sub> и Co<sub>3</sub> — подгруппы Co<sub>0</sub>, [[Действие группы#Стабилизаторы|стабилизаторы]] определённых векторов решётки. Эти группы вместе называют [[Группы Конвея|группами Конвея]]{{sfn|Wilson|2009|loc=5.4 The Leech lattice and the Conway group}}<ref group="JHC">{{публикация|статья |автор= J. H. Conway |заглавие= A Perfect Group of Order 8,315,553,613,086,720,000 and the Sporadic Simple Groups |издание= Bull. London Math. Soc. | издание nodot=1 |volume=1 |pages=79—88 |год=1969 |doi=10.1112/blms/1.1.79}}</ref><ref group="JHC">{{публикация|статья |автор= J. H. Conway |заглавие= A Group of Order 8,315,553,613,086,720,000 |издание= PNAS |volume=61 |pages=398—400 |год=1968 |doi= 10.1073/pnas.61.2.398 }}</ref>. |
Одно из самых важных достижений Конвея — исследование [[Группа автоморфизмов|группы автоморфизмов]] [[Решётка Лича|решётки Лича]] Co<sub>0</sub>. Он нашёл, что эта группа имеет порядок {{nobr|8 315 553 613 086 720 000}} и включает три новые спорадические группы [[Группа Конвея Co1|Co<sub>1</sub>]], Co<sub>2</sub>, Co<sub>3</sub> (их простота была впервые показана Джоном Томпсоном; Co<sub>0</sub> включает и некоторые другие спорадические группы, открытые незадолго до того{{sfn|Ronan|2006|p=155}}): Co<sub>1</sub> — [[факторгруппа]] Co<sub>0</sub> по её [[Центр группы|центру]], единственным нетривиальным элементом которого является домножение на −1, Co<sub>2</sub> и Co<sub>3</sub> — подгруппы Co<sub>0</sub>, [[Действие группы#Стабилизаторы|стабилизаторы]] определённых векторов решётки. Эти группы вместе называют [[Группы Конвея|группами Конвея]]{{sfn|Wilson|2009|loc=5.4 The Leech lattice and the Conway group}}<ref group="JHC">{{публикация|статья |автор= J. H. Conway |заглавие= A Perfect Group of Order 8,315,553,613,086,720,000 and the Sporadic Simple Groups |издание= Bull. London Math. Soc. | издание nodot=1 |volume=1 |pages=79—88 |год=1969 |doi=10.1112/blms/1.1.79}}</ref><ref group="JHC">{{публикация|статья |автор= J. H. Conway |заглавие= A Group of Order 8,315,553,613,086,720,000 |издание= PNAS |volume=61 |pages=398—400 |год=1968 |doi= 10.1073/pnas.61.2.398 }}</ref>. |
||
Он исследовал и другие спорадические группы |
Он исследовал и другие спорадические группы. В частности, вместе с Дэвидом Уэльсом впервые разработал построение [[Группа Рудвалиса|группы Рудвалиса Ru]]{{sfn|Wilson|2009|loc=5.9.3 The Rudvalis group}}<ref group="JHC">{{публикация|статья |автор= J. H. Conway and D. B. Wales |заглавие= The construction of the Rudvalis simple group of order 145,926,144,000 |издание= Journal of Algebra |volume=27 |pages=538—548 |год=1973 |doi=10.1016/0021-8693(73)90063-X}}</ref>. Также вместе с различными соавторами упростил построение различных групп, которые были построены или предсказаны другими авторами, например, ввёл построение [[Группа Фишера|группы Фишера Fi<sub>22</sub>]] через 77-мерное [[Представление группы|представление]] над [[Конечное поле#Поле из трёх элементов|полем из трёх элементов]]{{sfn|Wilson|2009|loc=5.7.3 Conway’s description of Fi<sub>22</sub>}}. |
||
==== Чудовищный вздор ==== |
==== Чудовищный вздор ==== |
||
{{main|Monstrous moonshine}} |
|||
Особенное значение имеет работа Конвея над монстром, проделанная в период, когда существование этой группы ещё не было доказано, но о её свойствах уже было многое известно. |
Особенное значение имеет работа Конвея над [[Монстр (группа)|монстром]], проделанная в период, когда существование этой группы ещё не было доказано, но о её свойствах уже было многое известно. |
||
Джон Маккей и другие авторы сделали ряд наблюдений о структуре монстра и некоторых других групп и определённых численных совпадениях, в частности, о том, что коэффициенты фурье-разложения модулярной функции ''j''-инварианта представляются простыми линейными комбинациями размерностей представлений монстра. Джон Томпсон предложил рассмотреть степенные ряды с коэффициентами, являющимися [[Характер представления группы|характерами представлений]] монстра, вычисленными для различных его элементов. Конвей и Саймон Нортон развили эти наблюдения, построили такие функции (ряды Маккея — Томпсона) и обнаружили, что они похожи на модулярные функции особого вида, известные как {{lang-de|Hauptmodul}}. Они сформулировали гипотезу, что каждый ряд Маккея — Томпсона действительно соответствует определённому ''Hauptmodul'', что подразумевало глубокую и загадочную связь между спорадическими группами и модулярными функциями. Эта гипотеза получила название «гипотеза чудовищного вздора» — {{lang-en|monstrous moonshine}}<ref name="Ronan17" /><ref group="JHC">{{публикация|статья |автор= J. H. Conway and S. P. Norton |заглавие= Monstrous Moonshine |издание= Bull. London Math. Soc. | издание nodot=1 |volume=11 |pages=308—339 |год=1979 |doi=10.1112/blms/11.3.308}}</ref>. |
Джон Маккей и другие авторы сделали ряд наблюдений о структуре монстра и некоторых других групп и определённых численных совпадениях, в частности, о том, что коэффициенты фурье-разложения модулярной функции ''j''-инварианта представляются простыми линейными комбинациями размерностей представлений монстра. Джон Томпсон предложил рассмотреть степенные ряды с коэффициентами, являющимися [[Характер представления группы|характерами представлений]] монстра, вычисленными для различных его элементов. Конвей и Саймон Нортон развили эти наблюдения, построили такие функции (ряды Маккея — Томпсона) и обнаружили, что они похожи на модулярные функции особого вида, известные как {{lang-de|Hauptmodul}}. Они сформулировали гипотезу, что каждый ряд Маккея — Томпсона действительно соответствует определённому ''Hauptmodul'', что подразумевало глубокую и загадочную связь между спорадическими группами и модулярными функциями. Эта гипотеза получила название «гипотеза чудовищного вздора» — {{lang-en|monstrous moonshine}}<ref name="Ronan17" /><ref group="JHC">{{публикация|статья |автор= J. H. Conway and S. P. Norton |заглавие= Monstrous Moonshine |издание= Bull. London Math. Soc. | издание nodot=1 |volume=11 |pages=308—339 |год=1979 |doi=10.1112/blms/11.3.308}}</ref>. |
||
Гипотезу Конвея и Нортона доказал Ричард Борчердс с помощью [[Алгебра вершинных операторов|алгебр вершинных операторов]]. Однако сам Конвей и другие специалисты |
Гипотезу Конвея и Нортона доказал Ричард Борчердс с помощью [[Алгебра вершинных операторов|алгебр вершинных операторов]]. Однако сам Конвей и другие специалисты считали, что работа Борчердса хотя и формально доказывает гипотезу, но не объясняет её. Обнаруженные связи между алгебраическими объектами, такими как группы, и понятиями, связанными с модулярными функциями, были затем развиты и обобщены. Кроме того, оказалось, что эти связи могут быть сформулированы естественным образом на языке [[Конформная теория поля|конформных теорий поля]]. Все вместе эти наблюдения, гипотезы и теоремы называют просто «вздор» — ''moonshine''. В этой области ещё много открытых задач и неотвеченных вопросов{{sfn|Ronan|2006|loc=17 Moonshine|name=Ronan17}}<ref>{{публикация|книга|автор=Terry Gannon|заглавие=Moonshine Beyond the Monster|часть=0 Introduction: glimpses of the theory beneath Monstrous Moonshine|издательство=Cambridge University Press|год=2006|isbn=978-0-511-24514-5|isbn2=978-0-521-83531-2}}</ref>. |
||
==== [[Решётка (теория групп)|Решётки]] ==== |
==== [[Решётка (теория групп)|Решётки]] ==== |
||
Помимо конечных групп, Конвей исследовал также решётки и [[Плотная упаковка равных сфер|упаковки сфер]], а также близкую тему |
Помимо конечных групп, Конвей исследовал также решётки и [[Плотная упаковка равных сфер|упаковки сфер]], а также близкую тему [[Корректирующий код|кодов коррекции ошибок]]<ref group="JHC">{{публикация|статья |автор= J. H. Conway, R. H. Hardin and N. J. A. Sloane |заглавие= Packing Lines, Planes, etc.: Packings in Grassmannian Spaces |издание= Experimental Mathematics |volume=5 |pages=139—159 |год=1996 |doi= 10.1080/10586458.1996.10504585}}</ref>. В частности, он разработал новое построение для той же решётки Лича{{sfn|Thompson|1984|pp=123—127}}. Конвей и Нил Слоун изложили свои результаты и большое количество справочной информации в своей книге ''Sphere Packings, Lattices, and Groups''{{переход|SPLAG}}. |
||
==== [[Орбифолд]]ы, [[ |
==== [[Орбифолд]]ы, [[многогранник]]и и [[Замощение (геометрия)|замощения]] ==== |
||
[[Файл:Tiling p6m.svg|thumb|200px|Замощение плоскости, группа симметрии которого имеет орбифолдное обозначение *632]] |
[[Файл:Tiling p6m.svg|thumb|200px|Замощение плоскости, группа симметрии которого имеет орбифолдное обозначение *632]] |
||
Решётки, в свою очередь, связаны с темой [[Кристаллографическая группа|кристаллографических групп]] и замощений. |
Решётки, в свою очередь, связаны с темой [[Кристаллографическая группа|кристаллографических групп]] и замощений. |
||
В этой области важное достижение Конвея — популяризация и развитие придуманного Уильямом Тёрстоном подхода к изучению периодических групп симметрии [[Евклидово пространство|евклидова]], [[Гиперсфера|сферического]] и [[Гиперболическое пространство|гиперболического]] пространств. Этот подход имеет [[Топология|топологическую]] природу и основан на орбифолдах<ref name="Roberts14" />. Орбифолд — это [[топологическое пространство]], снабжённое определённой структурой, связанной с действием на него заданной конечной группы. Двумерные параболические орбифолды (те, у которых аналог [[Эйлерова характеристика|эйлеровой характеристики]] равен нулю) напрямую соответствуют [[Группа орнамента|двумерным кристаллографическим группам]]<ref>{{публикация|книга | заглавие = The Geometry and Topology of Three-Manifolds | автор = William P. Thurston | издательство = | год = | часть = Chapter 13. Orbifolds | часть ссылка = |
В этой области важное достижение Конвея — популяризация и развитие придуманного Уильямом Тёрстоном подхода к изучению периодических групп симметрии [[Евклидово пространство|евклидова]], [[Гиперсфера|сферического]] и [[Гиперболическое пространство|гиперболического]] пространств. Этот подход имеет [[Топология|топологическую]] природу и основан на орбифолдах<ref name="Roberts14" />. Орбифолд — это [[топологическое пространство]], снабжённое определённой структурой, связанной с действием на него заданной конечной группы. Двумерные параболические орбифолды (те, у которых аналог [[Эйлерова характеристика|эйлеровой характеристики]] равен нулю) напрямую соответствуют [[Группа орнамента|двумерным кристаллографическим группам]]<ref>{{публикация | книга | заглавие = The Geometry and Topology of Three-Manifolds | автор = William P. Thurston | издательство = | год = | часть = Chapter 13. Orbifolds | часть ссылка = https://library.slmath.org/books/gt3m/PDF/13.pdf | ссылка = https://library.slmath.org/books/gt3m/ | архив дата = 2023-10-18 | архив = https://web.archive.org/web/20231018183708/https://library.slmath.org/books/gt3m/ }}</ref>. На этом основана придуманная Конвеем и достаточно широко распространившаяся {{нп5|орбифолдная нотация|||Orbifold notation}} для этих и других подобных групп<ref>{{публикация|книга | заглавие = Discrete and Computational Geometry | ответственный = Ed. by Jacob E. Goodman, Joseph O'Rourke, and Csaba D. Tóth |издание=3rd edition| автор = Edmund Harriss, Doris Schattschneider, and Marjorie Senechal | издательство = CRC Press | год = 2017 | часть = Chapter 3. Tilings | часть ссылка =https://www.csun.edu/~ctoth/Handbook/chap3.pdf | isbn = 9781315119601 }}</ref><ref group="JHC">{{публикация|статья |автор= J. H. Conway and D. H. Hudson |заглавие= The Orbifold Notation for Two-Dimensional Groups |издание= Structural Chemistry |volume=13 |pages=247—257 |год=2002 |doi= 10.1023/A:1015851621002}}</ref>. Орбифолды связаны и с чудовищным вздором<ref>{{публикация|статья |автор=Michael P. Tuite |заглавие=Monstrous Moonshine from orbifolds |издание=Communications in Mathematical Physics |volume=146 |pages=277—309 |год=1992 |doi=10.1007/BF02102629}}</ref>. |
||
Известен [[критерий Конвея]] для плиток, замощающих плоскость. |
Известен [[критерий Конвея]] для плиток, замощающих плоскость. |
||
Тема замощений сферы непосредственно связана с многогранниками. Конвей придумал [[Нотация Конвея для многогранников|нотацию для многогранников]]<ref>{{cite web|url=http://www.georgehart.com/virtual-polyhedra/conway_notation.html|author=George W. Hart|title=Conway Notation for Polyhedra|website=Virtual Polyhedra|date=1998}}</ref> — ещё один пример его большой любви к изобретению и переизобретению названий и нотаций<ref name="Roberts14" />. Кроме того, Конвей и Майкл Гай перечислили все [[Четырёхмерный многогранник|четырёхмерные]] [[Архимедово тело|архимедовы тела]] и открыли {{нп5|Великая антипризма|великую антипризму||Grand antiprism}} — единственный [[Построение Витхоффа#Невитхоффово построение|невитхоффов]] однородный политоп<ref name="Roberts3" /><ref name="Princeton-dof" /><ref group="JHC">{{публикация|статья |автор= J. H. Conway and M. J. T. Guy |заглавие= Four-Dimensional Archimedean Polytopes |издание= Proceedings of the Colloquium on Convexity at Copenhagen |volume= |pages=38—39 |год=1965 |doi= }}</ref>. |
Тема замощений сферы непосредственно связана с многогранниками. Конвей придумал [[Нотация Конвея для многогранников|нотацию для многогранников]]<ref>{{cite web|url=http://www.georgehart.com/virtual-polyhedra/conway_notation.html|author=George W. Hart|title=Conway Notation for Polyhedra|website=Virtual Polyhedra|date=1998|access-date=2019-03-03|archive-date=2014-11-29|archive-url=https://web.archive.org/web/20141129085342/http://www.georgehart.com/virtual-polyhedra/conway_notation.html|deadlink=no}}</ref> — ещё один пример его большой любви к изобретению и переизобретению названий и нотаций<ref name="Roberts14" />. Кроме того, Конвей и Майкл Гай перечислили все [[Четырёхмерный многогранник|четырёхмерные]] [[Архимедово тело|архимедовы тела]] и открыли {{нп5|Великая антипризма|великую антипризму||Grand antiprism}} — единственный [[Построение Витхоффа#Невитхоффово построение|невитхоффов]] однородный политоп<ref name="Roberts3" /><ref name="Princeton-dof" /><ref group="JHC">{{публикация|статья |автор= J. H. Conway and M. J. T. Guy |заглавие= Four-Dimensional Archimedean Polytopes |издание= Proceedings of the Colloquium on Convexity at Copenhagen |volume= |pages=38—39 |год=1965 |doi= }}</ref>. |
||
==== Атлас ==== |
==== Атлас ==== |
||
Конвей известен как руководитель группы, собравшей «Атлас конечных групп» — грандиозный справочник, содержащий таблицы характеров конечных групп (не только спорадических) и ставший ценным инструментом для математиков, работавших с конечными группами в эпоху до развития [[интернет]]а<ref name="Roberts11" />. Сейчас Атлас существует в виде интернет-энциклопедии, сделанной командой под руководством Роберта Уилсона<ref>{{cite web|title=ATLAS of Finite Group Representations |
Конвей известен как руководитель группы, собравшей «Атлас конечных групп» — грандиозный справочник, содержащий таблицы характеров конечных групп (не только спорадических) и ставший ценным инструментом для математиков, работавших с конечными группами в эпоху до развития [[интернет]]а<ref name="Roberts11" />. Сейчас Атлас существует в виде интернет-энциклопедии, сделанной командой под руководством Роберта Уилсона<ref>{{cite web|title=ATLAS of Finite Group Representations|url=https://brauer.maths.qmul.ac.uk/Atlas/|accessdate=2023-10-18|archive-date=2023-05-18|archive-url=https://web.archive.org/web/20230518125351/https://brauer.maths.qmul.ac.uk/Atlas/|deadlink=no}}</ref>. |
||
=== [[Комбинаторная теория игр]] === |
=== [[Комбинаторная теория игр]] === |
||
Вклад Конвея в комбинаторную теорию игр — одно из самых известных его достижений<ref name="Princeton-dof">{{cite web|title=John Horton Conway|url=https://dof.princeton.edu/ |
Вклад Конвея в комбинаторную теорию игр — одно из самых известных его достижений<ref name="Princeton-dof">{{cite web|title=John Horton Conway|url=https://dof.princeton.edu/people/john-horton-conway|website=Princeton University|accessdate=2023-04-24|archive-date=2023-04-24|archive-url=https://web.archive.org/web/20230424145046/https://dof.princeton.edu/people/john-horton-conway|deadlink=no}}</ref>. |
||
[[Файл:Hackenbush girl.svg|thumb|150px|left|Игра хакенбуш: один игрок перерезает синие рёбра графа, другой — красные; фрагменты графа, отсоединённые от основания, исчезают целиком; проигрывает тот, кто не может сделать ход.]] |
[[Файл:Hackenbush girl.svg|thumb|150px|left|Игра хакенбуш: один игрок перерезает синие рёбра графа, другой — красные; фрагменты графа, отсоединённые от основания, исчезают целиком; проигрывает тот, кто не может сделать ход.]] |
||
| Строка 151: | Строка 161: | ||
=== [[Клеточные автоматы]] === |
=== [[Клеточные автоматы]] === |
||
[[Файл:Gospers glider gun.gif|thumb|300px|[[Планер (конфигурация клеточного автомата)|Глайдерная]] пушка в игре «Жизнь»]] |
[[Файл:Gospers glider gun.gif|thumb|300px|[[Планер (конфигурация клеточного автомата)|Глайдерная]] [[Ружьё (конфигурация клеточного автомата)|пушка]] в игре «Жизнь»]] |
||
Джон Конвей придумал [[Игра «Жизнь»|игру «Жизнь»]] — известный клеточный автомат. Он определён на поле, [[Квадратный паркет|замощённом квадратами]]. Каждая клетка поля в каждый момент ([[Дискретность|дискретного]]) времени считается живой либо мёртвой, причём на следующем временно́м шаге состояние клетки определяется следующими правилами, зависящими от состояния [[Окрестность Мура|её восьми клеток-соседей]] на текущем шаге<ref name="RobertsPrologue" />: |
Джон Конвей придумал [[Игра «Жизнь»|игру «Жизнь»]] — известный клеточный автомат. Он определён на поле, [[Квадратный паркет|замощённом квадратами]]. Каждая клетка поля в каждый момент ([[Дискретность|дискретного]]) времени считается живой либо мёртвой, причём на следующем временно́м шаге состояние клетки определяется следующими правилами, зависящими от состояния [[Окрестность Мура|её восьми клеток-соседей]] на текущем шаге<ref name="RobertsPrologue" />: |
||
* если клетка была живой, то она остаётся живой, если у неё было ровно 2 или 3 живых соседа; |
* если клетка была живой, то она остаётся живой, если у неё было ровно 2 или 3 живых соседа; |
||
| Строка 160: | Строка 170: | ||
Конвей подобрал правила игры «Жизнь» так, что начальные конфигурации даже из небольшого количества клеток развиваются зачастую совершенно непредсказуемо. Как затем оказалось, на поле игры «Жизнь» могут существовать [[Натюрморт (конфигурация клеточного автомата)|неподвижные]], [[Космический корабль (конфигурация клеточного автомата)|стабильно перемещающиеся]], [[Ружьё (конфигурация клеточного автомата)|стабильно размножающиеся]] конфигурации, [[Логический вентиль|логические вентили]], позволяющие реализовать в ней произвольное вычисление ([[полнота по Тьюрингу]]), и многие другие нетривиальные конструкции. Возможно множество вариантов и обобщений игры «Жизнь»{{sfn|Adamatzky|2010}}. |
Конвей подобрал правила игры «Жизнь» так, что начальные конфигурации даже из небольшого количества клеток развиваются зачастую совершенно непредсказуемо. Как затем оказалось, на поле игры «Жизнь» могут существовать [[Натюрморт (конфигурация клеточного автомата)|неподвижные]], [[Космический корабль (конфигурация клеточного автомата)|стабильно перемещающиеся]], [[Ружьё (конфигурация клеточного автомата)|стабильно размножающиеся]] конфигурации, [[Логический вентиль|логические вентили]], позволяющие реализовать в ней произвольное вычисление ([[полнота по Тьюрингу]]), и многие другие нетривиальные конструкции. Возможно множество вариантов и обобщений игры «Жизнь»{{sfn|Adamatzky|2010}}. |
||
Появление игры «Жизнь» привело к огромному росту интереса к клеточным автоматам<ref name="RobertsPrologue" />. Клеточные автоматы, подобные игре «Жизнь», стали инструментом [[Моделирование|моделирования]] природных процессов<ref>{{публикация|книга|автор=Bastien Chopard, Michel Droz |заглавие=Cellular Automata Modeling of Physical Systems |издательство=Cambridge University Press |год=2005 |isbn=9780521673457}}</ref><ref>{{публикация|книга|автор=Andreas Deutsch, Sabine Dormann |заглавие=Cellular Automaton Modeling of Biological Pattern Formation |издательство=Springer Science & Business Media |год=2007 |isbn=9780817644154}}</ref>, способом генерации [[Математика и изобразительное искусство|красивых изображений]]<ref>{{публикация|книга|заглавие=Designing Beauty: The Art of Cellular Automata|ответственный=A. Adamatzky, G. J. Martínez (Eds.)|издательство=Springer International Publishing|год=2016|isbn=978-3-319-27270-2 |isbn2= 978-3-319-27269-6|серия=Emergence, Complexity and Computation|серия volume=20}}</ref> и популярным упражнением по [[Программирование|программированию]]<ref>{{публикация| |
Появление игры «Жизнь» привело к огромному росту интереса к клеточным автоматам<ref name="RobertsPrologue" />. Клеточные автоматы, подобные игре «Жизнь», стали инструментом [[Моделирование|моделирования]] природных процессов<ref>{{публикация|книга|автор=Bastien Chopard, Michel Droz |заглавие=Cellular Automata Modeling of Physical Systems |издательство=Cambridge University Press |год=2005 |isbn=9780521673457}}</ref><ref>{{публикация|книга|автор=Andreas Deutsch, Sabine Dormann |заглавие=Cellular Automaton Modeling of Biological Pattern Formation |издательство=Springer Science & Business Media |год=2007 |isbn=9780817644154}}</ref>, способом генерации [[Математика и изобразительное искусство|красивых изображений]]<ref>{{публикация|книга|заглавие=Designing Beauty: The Art of Cellular Automata|ответственный=A. Adamatzky, G. J. Martínez (Eds.)|издательство=Springer International Publishing|год=2016|isbn=978-3-319-27270-2 |isbn2= 978-3-319-27269-6|серия=Emergence, Complexity and Computation|серия volume=20}}</ref> и популярным упражнением по [[Программирование|программированию]]<ref>{{публикация|1=статья|автор=Michael M. Skolnick, David L. Spooner|заглавие=Graphical User Interface in Introductory Computer Science|издание=NECC '95, Baltimore, MD|год=1995|ссылка=https://eric.ed.gov/?id=ED392437|pages=279—285|архив дата=2021-08-09|архив=https://web.archive.org/web/20210809151148/https://eric.ed.gov/?id=ED392437}}</ref>. |
||
Вокруг игры «Жизнь» сразу сложилось сообщество энтузиастов-исследователей<ref name="Roberts9" />. Такое сообщество существует и сейчас, обмениваясь информацией о новых открытиях на сайте [ |
Вокруг игры «Жизнь» сразу сложилось сообщество энтузиастов-исследователей<ref name="Roberts9" />. Такое сообщество существует и сейчас, обмениваясь информацией о новых открытиях на сайте [https://conwaylife.com/ ConwayLife.com]<ref>{{публикация |1= статья |автор= Robert Bosch and Julia Olivieri |заглавие= Game-of-Life Mosaics |издание= Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture |pages= 325—328 |год= 2014 |ссылка= http://t.archive.bridgesmathart.org/2014/bridges2014-325.pdf |архив дата= 2019-03-27 |архив= https://web.archive.org/web/20190327085748/http://t.archive.bridgesmathart.org/2014/bridges2014-325.pdf }}</ref>. |
||
Среди клеточных автоматов несколько другого типа, придуманных в непосредственном окружении Конвея, можно также отметить [[Черви Патерсона|червей Патерсона]]<ref>{{MathWorld|PatersonsWorms|Paterson's Worms}}</ref>. |
Среди клеточных автоматов несколько другого типа, придуманных в непосредственном окружении Конвея, можно также отметить [[Черви Патерсона|червей Патерсона]]<ref>{{MathWorld|PatersonsWorms|Paterson's Worms}}</ref>. |
||
=== [[Теория чисел]] === |
=== [[Теория чисел]] === |
||
Конвей изобрёл тьюринг-полный [[эзотерический язык программирования]] |
Конвей изобрёл тьюринг-полный [[эзотерический язык программирования]] [[FRACTRAN]]. |
||
Программа на этом языке представляет собой упорядоченный набор [[Обыкновенная дробь|обыкновенных дробей]] и стартовое целое число. Чтобы выполнить программу, нужно последовательно умножать имеющееся целое число на первую такую дробь из набора, что в результате вновь получается целое число (тем самым возникающие целые числа формируют последовательность), до тех пор, пока это возможно<ref group="JHC">{{публикация |1=статья |автор=J. H. Conway |оригинал=FRACTRAN: A Simple Universal Programming Language for Arithmetic |заглавие=Фрактран: простой универсальный язык программирования для арифметики |ссылка=https://biblio.mccme.ru/sites/default/files/bookfiles/fraktran.pdf |издание=Open Problems Commun. Comput. |издание nodot=1 |volume= |pages=4—26 |год=1987 |doi=10.1007/978-1-4612-4808-8_2 |архив дата=2023-05-20 |архив=https://web.archive.org/web/20230520191725/https://biblio.mccme.ru/sites/default/files/bookfiles/fraktran.pdf }}</ref>. Так, Конвей приводит программу для генерации [[Простое число|простых чисел]]: |
|||
<math>\left( \frac{17}{91}, \frac{78}{85}, \frac{19}{51}, \frac{23}{38}, \frac{29}{33}, \frac{77}{29}, \frac{95}{23}, \frac{77}{19}, \frac{1}{17}, \frac{11}{13}, \frac{13}{11}, \frac{15}{2}, \frac{1}{7}, \frac{55}{1} \right)</math> |
<math>\left( \frac{17}{91}, \frac{78}{85}, \frac{19}{51}, \frac{23}{38}, \frac{29}{33}, \frac{77}{29}, \frac{95}{23}, \frac{77}{19}, \frac{1}{17}, \frac{11}{13}, \frac{13}{11}, \frac{15}{2}, \frac{1}{7}, \frac{55}{1} \right)</math> |
||
| Строка 178: | Строка 189: | ||
* положительно определённая квадратичная форма с целочисленной матрицей представляет все натуральные числа тогда и только тогда, когда она представляет все натуральные числа, меньшие либо равные 15; |
* положительно определённая квадратичная форма с целочисленной матрицей представляет все натуральные числа тогда и только тогда, когда она представляет все натуральные числа, меньшие либо равные 15; |
||
* положительно определённая квадратичная форма с целочисленными значениями представляет все натуральные числа тогда и только тогда, когда она представляет все натуральные числа, меньшие либо равные 290. |
* положительно определённая квадратичная форма с целочисленными значениями представляет все натуральные числа тогда и только тогда, когда она представляет все натуральные числа, меньшие либо равные 290. |
||
Эти утверждения родственны [[Теорема Лагранжа о сумме четырёх квадратов|теореме Лагранжа о сумме четырёх квадратов]] (как и несостоявшаяся первая диссертация Конвея{{переход|Начало научной и преподавательской карьеры|back}}). Конвей и Шнибергер доказали первое утверждение, но доказательство было сложным, и было опубликовано лишь в виде наброска в диссертации Шнибергера. Впоследствии [[Бхаргава, Манджул|Манджул Бхаргава]] упростил доказательство первой теоремы, обобщил её и доказал вторую теорему совместно с Дж. Ханке<ref>{{публикация|статья |автор= Alexander J. Hahn |заглавие= Quadratic Forms over ℤ from Diophantus to the 290 Theorem |издание= Advances in Applied Clifford Algebras |volume= 18 |pages= 665—676 |год= 2008 |doi= 10.1007/s00006-008-0090-y |ссылка = https://math.nd.edu/assets/20630/hahntoulouse.pdf}}</ref><ref group="JHC">{{публикация| |
Эти утверждения родственны [[Теорема Лагранжа о сумме четырёх квадратов|теореме Лагранжа о сумме четырёх квадратов]] (как и несостоявшаяся первая диссертация Конвея{{переход|Начало научной и преподавательской карьеры|back}}). Конвей и Шнибергер доказали первое утверждение, но доказательство было сложным, и было опубликовано лишь в виде наброска в диссертации Шнибергера. Впоследствии [[Бхаргава, Манджул|Манджул Бхаргава]] упростил доказательство первой теоремы, обобщил её и доказал вторую теорему совместно с Дж. Ханке<ref>{{публикация |1= статья |автор= Alexander J. Hahn |заглавие= Quadratic Forms over ℤ from Diophantus to the 290 Theorem |издание= Advances in Applied Clifford Algebras |volume= 18 |pages= 665—676 |год= 2008 |doi= 10.1007/s00006-008-0090-y |ссылка= https://math.nd.edu/assets/20630/hahntoulouse.pdf |архив дата= 2019-05-17 |архив= https://web.archive.org/web/20190517113039/https://math.nd.edu/assets/20630/hahntoulouse.pdf }}</ref><ref group="JHC">{{публикация|книга|автор= J. H. Conway |часть= Universal quadratic forms and the fifteen theorem |заглавие=Quadratic Forms and Their Applications|серия= Contemp. Math. |pages= 23—26 |год= 2000 |часть ссылка = http://www.fen.bilkent.edu.tr/~franz/mat/15.pdf |doi= 10.1090/conm/272/04394}}</ref>. |
||
Конвей придумал [[Стрелочные обозначения Конвея|стрелочные обозначения]] для очень больших чисел<ref name="Princeton-dof" />. |
Конвей придумал [[Стрелочные обозначения Конвея|стрелочные обозначения]] для очень больших чисел<ref name="Princeton-dof" />. |
||
| Строка 185: | Строка 196: | ||
=== [[Теория узлов]] === |
=== [[Теория узлов]] === |
||
[[Файл:RationalTangle 2 1 3.svg|thumb| |
[[Файл:RationalTangle 2 1 3.svg|thumb|180px|Поэтапное создание плетения — одного из ключевых объектов нотации Конвея для узлов]] |
||
Развив идеи {{нп5|Киркман, Томас|Томаса Киркмана||Thomas Kirkman}}, Конвей разработал [[Нотация Конвея для узлов|нотацию для узлов и зацеплений]], основанную на вставке определённых {{не переведено 5|Плетение (математика)|плетений||Tangle (mathematics)}} в вершины некоторых [[Регулярный граф|4-регулярных]] [[Планарный граф|планарных графов]]. Это позволило ему быстро и легко воспроизвести существовавшие таблицы узлов с небольшим [[Число пересечений (теория узлов)|числом пересечений]] и исправить большинство из ошибок этих таблиц<ref>{{публикация|книга|автор=Slavik V. Jablan and Radmila Sazdanovic |заглавие=Knot Theory and Its Applications |ответственный= ed. by Krishnendu Gongopadhyay and Rama Mishra |часть=From Conway Notation to LinKnot |издательство=AMS |год=2016 |isbn=978-1-4704-2257-8 |isbn2=978-1-4704-3526-4}}</ref><ref>{{публикация|книга|автор=J. Hoste |заглавие=Handbook of Knot Theory |ответственный= ed. by William Menasco and Morwen Thistlethwaite |часть= The enumeration and classification of knots and links| pages = 220 |издательство=Elsevier |год=2005 |isbn=9780080459547}}</ref><ref group="JHC">{{публикация|статья |автор= J. H. Conway |заглавие= An Enumeration of Knots and Links, and Some of Their Algebraic Properties |издание= Computational Problems in Abstract Algebra |volume= |pages=329—358 |год=1970 |doi= 10.1016/B978-0-08-012975-4.50034-5 }}</ref>. |
Развив идеи {{нп5|Киркман, Томас|Томаса Киркмана||Thomas Kirkman}}, Конвей разработал [[Нотация Конвея для узлов|нотацию для узлов и зацеплений]], основанную на вставке определённых {{не переведено 5|Плетение (математика)|плетений||Tangle (mathematics)}} в вершины некоторых [[Регулярный граф|4-регулярных]] [[Планарный граф|планарных графов]]. Это позволило ему быстро и легко воспроизвести существовавшие таблицы узлов с небольшим [[Число пересечений (теория узлов)|числом пересечений]] и исправить большинство из ошибок этих таблиц<ref>{{публикация|книга|автор=Slavik V. Jablan and Radmila Sazdanovic |заглавие=Knot Theory and Its Applications |ответственный= ed. by Krishnendu Gongopadhyay and Rama Mishra |часть=From Conway Notation to LinKnot |издательство=AMS |год=2016 |isbn=978-1-4704-2257-8 |isbn2=978-1-4704-3526-4}}</ref><ref>{{публикация|книга|автор=J. Hoste |заглавие=Handbook of Knot Theory |ответственный= ed. by William Menasco and Morwen Thistlethwaite |часть= The enumeration and classification of knots and links| pages = 220 |издательство=Elsevier |год=2005 |isbn=9780080459547}}</ref><ref group="JHC">{{публикация|статья |автор= J. H. Conway |заглавие= An Enumeration of Knots and Links, and Some of Their Algebraic Properties |издание= Computational Problems in Abstract Algebra |volume= |pages=329—358 |год=1970 |doi= 10.1016/B978-0-08-012975-4.50034-5 }}</ref>. |
||
Кроме того, он разработал свой вариант [[Многочлен Александера — Конвея|многочлена Александера]] — полиномиального [[Инвариант узла|инварианта узлов]] — и обратил внимание на важность [[Скейн-соотношение|скейн-соотношений]], которые затем стали распространённым удобным способом определения полиномиальных инвариантов узлов<ref>{{публикация|книга|автор=M. Epple |часть= Geometric aspects in the development of knot theory |заглавие= History of Topology |ответственный= ed. by I. M. James| pages = 309 |издательство=Elsevier |год=1999 |isbn=9780080534077}}</ref>. |
Кроме того, он разработал свой вариант [[Многочлен Александера — Конвея|многочлена Александера]] — полиномиального [[Инвариант узла|инварианта узлов]] — и обратил внимание на важность [[Скейн-соотношение|скейн-соотношений]], которые затем стали распространённым удобным способом определения полиномиальных инвариантов узлов<ref>{{публикация|книга|автор=M. Epple |часть= Geometric aspects in the development of knot theory |заглавие= History of Topology |ответственный= ed. by I. M. James| pages = 309 |издательство=Elsevier |год=1999 |isbn=9780080534077}}</ref>. |
||
Конвей нашёл названный в честь него [[Узел Конвея|узел]] с 11 пересечениями, примечательный тем, что некоторые вопросы теории узлов применительно к нему оказываются особенно сложными<ref>{{cite web|author=Erica Klarreich|title=Graduate Student Solves Decades-Old Conway Knot Problem|url=https://www.quantamagazine.org/graduate-student-solves-decades-old-conway-knot-problem-20200519/|website=Quanta Magazine|date=2020-05-19|accessdate=2023-06-03|archive-date=2021-04-17|archive-url=https://web.archive.org/web/20210417081123/https://www.quantamagazine.org/graduate-student-solves-decades-old-conway-knot-problem-20200519/|deadlink=no}}</ref>. |
|||
=== [[Квантовая механика]] === |
=== [[Квантовая механика]] === |
||
Совместно с Саймоном Кошеном Конвей доказал |
Совместно с Саймоном Кошеном Конвей доказал [[Теорема о свободе воли|теорему о свободе воли]]. Теорема опирается на несколько базовых постулатов квантовой теории. Согласно теореме, если у экспериментаторов есть свобода воли, то она есть и у элементарных частиц. Под намеренно провокационным термином «[[свобода воли]]» понимается спонтанное поведение, которое принципиально не определяется заранее. Тем самым теорема отвергает [[Теория скрытых параметров|теории скрытых параметров]] и [[детерминизм]]. Многие физики сочли, что теорема не привносит ничего существенно нового, но в философии она вызвала заметное обсуждение{{sfn|Roberts|2015|loc=13. Mortality Flash|name=Roberts13}}<ref>{{публикация|книга|автор= F. Scardigli |заглавие= Determinism and Free Will |ответственный= Fabio Scardigli, Gerard 't Hooft, Emanuele Severino, Piero Coda |часть= Introduction| pages = 10 |издательство= Springer |год=2019 |isbn= 9783030055059}}</ref><ref group="JHC">{{публикация|статья |автор= J. H. Conway and S. Kochen |заглавие= The Free Will Theorem |издание= Foundations of Physics |volume= 36 |pages=1441—1473 |год=2006 |doi= 10.1007/s10701-006-9068-6 |arxiv= quant-ph/0604079 }}</ref>. |
||
=== [[Занимательная математика]] === |
=== [[Занимательная математика]] === |
||
Конвей |
Конвей тратил значительное время на занятия, которые многие сочли бы бесполезной тратой усилий<ref name="RobertsPrologue" />. Возможно, самый характерный пример — изобретённый им [[алгоритм Судного дня]] для определения дня недели для заданной даты. Конвей потратил очень много времени как на упрощение алгоритма, так и на тренировку своего навыка его использования<ref name="Roberts11" /><ref name="Roberts13" />. Он интересовался и хорошо изученными областями, в которых трудно получить новый результат, такими как [[геометрия треугольника]] — так, он упростил доказательство [[Теорема Морли|теоремы Морли]]<ref name="Roberts14" />. Не чуждался и головоломок — известна [[головоломка Конвея]]. Изучение разнообразных числовых последовательностей тоже зачастую ближе к занимательной математике, чем к реальной науке — хотя, к примеру, результаты о последовательностях типа фигурирующей в гипотезе Коллатца действительно нетривиальны и представляют общий интерес, это едва ли можно сказать о таких исследованных Конвеем известных последовательностях, как ''RATS'' и ''subprime Fibonacci''<ref>{{публикация|статья |автор= Richard K. Guy, Tanya Khovanova, Julian Salazar |заглавие= Conway's subprime Fibonacci sequences |издание= Mathematics Magazine |volume= 87 |pages= 323—337 |год= 2014 |doi = 10.4169/math.mag.87.5.323 |arxiv= 1207.5099}}</ref>. Интересы Конвея простирались и в такие темы, как [[еврейский календарь]] и [[этимология]] необычных английских слов<ref name="Princeton-dof" />. Разграничить глубокую научную работу и легкомысленные развлечения в деятельности Конвея зачастую невозможно<ref name="magus">{{публикация|статья|автор=Richard K. Guy|заглавие=John Horton Conway: Mathematical Magus|издание=The Two-Year College Mathematics Journal|год=1982| doi=10.2307/3026500 |issue=5|volume=13|pages=290—299}}</ref>. Довольно запутан в этом отношении и статус некоторых его известных работ, упомянутых выше (это связано и с тем, что его самого этот вопрос не заботил): комбинаторная теория игр изначально воспринималась в основном как развлечение и лишь со временем приобрела более веский статус<ref name="Siegel" />, а клеточные автоматы значительная часть научного сообщества всегда воспринимала как область занимательной математики без какого-либо глубокого теоретического значения<ref>{{публикация|книга|автор= T. Bolognesi |заглавие= Advances in Unconventional Computing: Volume 1: Theory |ответственный= ed. by Andrew Adamatzky |часть= Spacetime Computing: Towards Algorithmic Causal Sets with Special-Relativistic Properties | pages = 272—273 |издательство= Springer |год=2016 |isbn= 9783319339245}}</ref>. |
||
=== Научное руководство === |
=== Научное руководство === |
||
Степень [[Доктор философии|PhD]] под руководством Конвея получили более двух десятков аспирантов, включая будущего [[Филдсовская премия|филдсовского лауреата]] Ричарда Борчердса<ref name="MathGen">{{MathGenealogy|id=18849|title=Джон Хортон Конвей}}</ref>. |
Степень [[Доктор философии|PhD]] под руководством Конвея получили более двух десятков аспирантов, включая будущего [[Филдсовская премия|филдсовского лауреата]] [[Борчердс, Ричард|Ричарда Борчердса]]<ref name="MathGen">{{MathGenealogy|id=18849|title=Джон Хортон Конвей}}</ref>. |
||
== Признание == |
== Признание == |
||
[[Файл:Gateknot.jpg|thumb|210px|Узел Конвея на воротах Института Исаака Ньютона в Кембридже<ref>{{cite web|title=Mathematical Gates (Faulkes Gatehouse)|url=https://www.newton.ac.uk/about/art-artefacts/mathematical-gates-faulkes-gatehouse/|website=Isaac Newton Institute for Mathematical Sciences|accessdate=2022-02-17|archive-date=2021-06-13|archive-url=https://web.archive.org/web/20210613230204/https://www.newton.ac.uk/about/art-artefacts/mathematical-gates-faulkes-gatehouse/|deadlink=no}}</ref>]] |
|||
* {{iw|Премия Бервика||en|Berwick Prize}} (1971)<ref name="LMS Prize Winners">{{cite web|title=List of LMS prize winners|url=https://www.lms.ac.uk/prizes/list-lms-prize-winners|website=London Mathematical Society|accessdate=2019-02-15}}</ref> |
* {{iw|Премия Бервика||en|Berwick Prize}} (1971)<ref name="LMS Prize Winners">{{cite web|title=List of LMS prize winners|url=https://www.lms.ac.uk/prizes/list-lms-prize-winners|website=London Mathematical Society|accessdate=2019-02-15|archive-date=2019-09-30|archive-url=https://web.archive.org/web/20190930160751/https://www.lms.ac.uk/prizes/list-lms-prize-winners|deadlink=no}}</ref> |
||
* Избран членом [[Лондонское королевское общество|Лондонского королевского общества]] (1981)<ref>{{cite web|title=John Conway|url=https://royalsociety.org/people/john-conway-11257/|website=Royal Society|accessdate=2019-02-15}}</ref> |
* Избран членом [[Лондонское королевское общество|Лондонского королевского общества]] (1981)<ref>{{cite web|title=John Conway|url=https://royalsociety.org/people/john-conway-11257/|website=Royal Society|accessdate=2019-02-15|archive-date=2019-03-21|archive-url=https://web.archive.org/web/20190321220441/https://royalsociety.org/people/john-conway-11257/|deadlink=no}}</ref> |
||
* {{iw|Премия Пойа||en|Pólya Prize (LMS)}} (1987)<ref name="LMS Prize Winners" /> |
* {{iw|Премия Пойа||en|Pólya Prize (LMS)}} (1987)<ref name="LMS Prize Winners" /> |
||
* Избран членом [[Американская академия искусств и наук|Американской академии искусств и наук]] (1992)<ref>{{cite web|title=John Horton Conway|url=https://www.amacad.org/person/john-horton-conway|website=American Academy of Arts and Sciences|accessdate=2020-04-16|archive-date=2020-04-12|archive-url=https://web.archive.org/web/20200412194626/https://www.amacad.org/person/john-horton-conway|deadlink=no}}</ref> |
|||
* [[Премия Неммерса по математике]] (1998)<ref>{{cite web|title= |
* [[Премия Неммерса по математике]] (1998)<ref>{{cite web|title=Past Winners: Nemmers Prize|website=Northwestern University|url=https://www.nemmers.northwestern.edu/past-winners/#tab-panel3|accessdate=2024-02-16|archive-date=2023-12-02|archive-url=https://web.archive.org/web/20231202182603/https://www.nemmers.northwestern.edu/past-winners/#tab-panel3|deadlink=no}}</ref> |
||
* [[Премия Стила]] (2000)<ref>{{cite web|url=http://www.ams.org/notices/200004/comm-steele.pdf|title=2000 Steele Prizes|author=|date=|publisher=American Mathematical Society|accessdate=2013-08-09|lang=en|archiveurl=https://www.webcitation.org/6JEVIGccS?url=http://www.ams.org/notices/200004/comm-steele.pdf|archivedate=2013-08-29}}</ref> |
|||
* Премия |
* [[Премия Стила]] (2000)<ref>{{cite web|url=https://www.ams.org/notices/200004/comm-steele.pdf|title=2000 Steele Prizes|author=|date=|publisher=American Mathematical Society|accessdate=2013-08-09|lang=en|archiveurl=https://web.archive.org/web/20220121224246/https://www.ams.org/notices/200004/comm-steele.pdf|archivedate=2022-01-21}}</ref> |
||
* Премия Джозефа Пристли (2000-01)<ref>{{cite web |title= Joseph Priestley Award |url= https://www.dickinson.edu/info/20043/about/1973/dickinson_awards/2 |accessdate= 2019-03-15 |archive-date= 2019-04-21 |archive-url= https://web.archive.org/web/20190421080432/https://www.dickinson.edu/info/20043/about/1973/dickinson_awards/2 |deadlink= no }}</ref> |
|||
* Многочисленные [[Honoris causa|почётные научные степени]]{{sfn|Roberts|2015|loc=Epilogue|name=RobertsEpilogue}} |
* Многочисленные [[Honoris causa|почётные научные степени]]{{sfn|Roberts|2015|loc=Epilogue|name=RobertsEpilogue}} |
||
В 2015 году вышла биография Конвея — книга Шивон Робертс «Genius at Play: The Curious Mind of John Horton Conway» ({{sfn0|Roberts|2015}})<ref name="ORourke" /><ref>{{cite web|title=Reviews § Genius at Play: The Curious Mind of John Horton Conway, by Siobhan Roberts|url=https://www.ams.org/media-reviews#genius|website=AMS|accessdate=2022-02-17|archive-date=2020-02-03|archive-url=https://web.archive.org/web/20200203171722/https://www.ams.org/media-reviews|deadlink=no}}</ref>. |
|||
== Библиография == |
== Библиография == |
||
Библиография Конвея включает около 100 статей в научных журналах, несколько десятков статей в научно-популярных изданиях и трудах конференций и 9 книг. Список публикаций в научных математических изданиях за всё время и список публикаций во всех научных изданиях приблизительно с начала 1970-х годов имеются в базах данных [https://www.zbmath.org/authors/?q=ai:conway.john-horton zbMATH] и [http://www.scopus.com/authid/detail.url?authorId=55322875100 Scopus], соответственно. Полный список публикаций за период до 1999 года доступен на сайте Принстонского университета<ref>{{cite web|title=John Horton Conway. Bibliography|url=https://www.math.princeton.edu/sites/default/files/2017-03/ConwayBIB1.pdf|website=Princeton University Department of Mathematics|accessdate=2019-03-06|description=Список книг не совсем верен|archive-date=2019-05-17|archive-url=https://web.archive.org/web/20190517113045/https://www.math.princeton.edu/sites/default/files/2017-03/ConwayBIB1.pdf|deadlink=no}}</ref>. Избранная библиография приведена в книге {{sfn0|Roberts|2015}}. |
|||
=== Книги === |
=== Книги === |
||
| Строка 221: | Строка 238: | ||
* {{якорь2|SPLAG|текст={{публикация|книга|автор=J. H. Conway, N. J. A. Sloane|заглавие=Sphere Packings, Lattices, and Groups|место=New York|издательство=Springer-Verlag|год=1988|isbn=9780387966175}}}} |
* {{якорь2|SPLAG|текст={{публикация|книга|автор=J. H. Conway, N. J. A. Sloane|заглавие=Sphere Packings, Lattices, and Groups|место=New York|издательство=Springer-Verlag|год=1988|isbn=9780387966175}}}} |
||
** Русский перевод первого издания: {{публикация|книга|автор=Конвей Дж., Слоэн Н.|заглавие=Упаковки шаров, решётки и группы|место=М.|издательство=Мир|год=1990|isbn=9785030023687 (том 1)|isbn2=9785030023694 (том 2)}} |
** Русский перевод первого издания: {{публикация|книга|автор=Конвей Дж., Слоэн Н.|заглавие=Упаковки шаров, решётки и группы|место=М.|издательство=Мир|год=1990|isbn=9785030023687 (том 1)|isbn2=9785030023694 (том 2)}} |
||
** Третье издание: {{публикация|книга|автор=J. H. Conway, N. J. A. Sloane|заглавие=Sphere Packings, Lattices, and Groups|издание=3rd ed.|место=New York|издательство=Springer-Verlag|год=1999|isbn=9781475720167|isbn2=9781475720167}} |
** Третье издание: {{публикация|книга|автор=J. H. Conway, N. J. A. Sloane|заглавие=Sphere Packings, Lattices, and Groups|издание=3rd ed.|место=New York|издательство=Springer-Verlag|год=1999|isbn=9781475720167|isbn2=9781475720167 |примечание= [http://neilsloane.com/doc/splag.html Errata]}} |
||
* {{публикация|книга|автор=J. H. Conway, Richard K. Guy|заглавие=The Book of Numbers|издательство=Springer-Verlag|место=New York|год=1996|isbn=0614971667}} |
* {{публикация|книга|автор=J. H. Conway, Richard K. Guy|заглавие=The Book of Numbers|издательство=Springer-Verlag|место=New York|год=1996|isbn=0614971667}} |
||
* {{публикация|книга|автор=J. H. Conway assisted by Francis Y. C. Fung|заглавие=The Sensual (Quadratic) Form|издательство=MAA|год=1997|isbn=9780883850305}} |
* {{публикация|книга|автор=J. H. Conway assisted by Francis Y. C. Fung|заглавие=The Sensual (Quadratic) Form|издательство=MAA|год=1997|isbn=9780883850305}} |
||
** Русский перевод: {{публикация|книга|автор=Конвей Дж.|заглавие=Квадратичные формы, данные нам в ощущениях|место=М.|издательство=МЦНМО|год=2008|isbn=9785940572688}} |
** Русский перевод: {{публикация|книга|автор=Конвей Дж.|заглавие=Квадратичные формы, данные нам в ощущениях|место=М.|издательство=МЦНМО|год=2008|isbn=9785940572688}} |
||
* {{публикация|книга|автор=John H. Conway, Derek A. Smith|заглавие=On Quaternions and Octonions|подзаголовок=Their geometry, arithmetic, and symmetry|издательство=Taylor & Francis|год=2003|isbn=9781439864180}} |
* {{публикация|книга|автор=John H. Conway, Derek A. Smith|заглавие=On Quaternions and Octonions|подзаголовок=Their geometry, arithmetic, and symmetry|издательство=Taylor & Francis|год=2003|isbn=9781439864180 |примечание= [https://sites.lafayette.edu/smithder/files/2012/12/QANDOErrata.pdf Errata]}} |
||
** Русский перевод: {{публикация|книга|автор=Конвей Дж., Смит Д.|заглавие=О кватернионах и октавах, об их геометрии, арифметике и симметриях|место=М.|издательство=МЦНМО|год=2009|isbn=9785940575177}} |
** Русский перевод: {{публикация|книга|автор=Конвей Дж., Смит Д.|заглавие=О кватернионах и октавах, об их геометрии, арифметике и симметриях|место=М.|издательство=МЦНМО|год=2009|isbn=9785940575177}} |
||
* {{публикация|книга|автор=John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss|заглавие=The Symmetries of Things|издательство=Taylor & Francis|год=2008|isbn=9781568812205 |примечание= [http://www.mit.edu/~hlb/Symmetries_of_Things/SoTerrors.html Errata]}} |
* {{публикация|книга|автор=John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss|заглавие=The Symmetries of Things|издательство=Taylor & Francis|год=2008|isbn=9781568812205 |примечание= [http://www.mit.edu/~hlb/Symmetries_of_Things/SoTerrors.html Errata]}} |
||
=== Некоторые статьи === |
=== Некоторые статьи === |
||
Избранные статьи Конвея опубликованы на русском языке в сборнике «[[#сборник|Человек, который играл в математику]]». |
|||
{{примечания|group=JHC}} |
{{примечания|group=JHC}} |
||
| Строка 237: | Строка 255: | ||
== Литература == |
== Литература == |
||
{{Навигация}} |
{{Навигация}} |
||
=== О Конвее === |
|||
* {{публикация|книга|автор=Siobhan Roberts|заглавие=Genius At Play. The Curious Mind of John Horton Conway|издательство=Bloomsbury USA|год=2015|isbn=9781620405932|ref=Roberts}} |
* {{публикация|книга|автор=Siobhan Roberts|заглавие=Genius At Play. The Curious Mind of John Horton Conway|издательство=Bloomsbury USA|год=2015|isbn=9781620405932|ссылка=https://siobhanroberts.com/genius-at-play/|примечание=[https://siobhanroberts.com/genius-at-play/errata/ Errata]|ref=Roberts}} |
||
* {{cite web|author=Siobhan Roberts|title=A Life in Games|url=https://www.quantamagazine.org/john-conways-life-in-games-20150828|website=Quanta Magazine|date=2015-08-28|accessdate=2020-06-04}} Перевод: [https://habr.com/ru/post/274081/ Джон Хортон Конвей: Жизнь, как игра]. |
|||
=== Математическая литература === |
|||
* {{якорь2|сборник|текст={{публикация|книга|заглавие=Человек, который играл в математику. Сборник памяти Джона Конвея|ответственный=пер. с англ. Б. Р. Френкина|издательство=МЦНМО|год=2023|isbn=978-5-4439-1787-0}}}} |
|||
* {{публикация|книга|автор=Thomas M. Thompson|заглавие=From Error-Correcting Codes through Sphere Packings to Simple Groups|издательство=MAA|год=1984|ref=Thompson}} |
* {{публикация|книга|автор=Thomas M. Thompson|заглавие=From Error-Correcting Codes through Sphere Packings to Simple Groups|издательство=MAA|год=1984|ref=Thompson}} |
||
* {{публикация|книга|автор=Mark Ronan|заглавие=Symmetry and the Monster|издательство=Oxford University Press|год=2006|isbn=9780192807229|ref=Ronan}} |
* {{публикация|книга|автор=Mark Ronan|заглавие=Symmetry and the Monster|издательство=Oxford University Press|год=2006|isbn=9780192807229|ref=Ronan}} |
||
* {{публикация|книга|автор=Robert A. Wilson|заглавие=The Finite Simple Groups|издательство=Springer|год=2009|isbn=978-1-84800-987-5|isbn2=978-1-84800-988-2 |примечание= [http://www.maths.qmul.ac.uk/~raw/TFSG.html Addenda and corrigenda] |ref=Wilson}} |
* {{публикация|книга|автор=Robert A. Wilson|заглавие=The Finite Simple Groups|издательство=Springer|год=2009|isbn=978-1-84800-987-5|isbn2=978-1-84800-988-2 |примечание= [https://web.archive.org/web/20220111092534/http://www.maths.qmul.ac.uk/~raw/TFSG.html Addenda and corrigenda] |ref=Wilson}} |
||
* {{публикация|книга|автор=Aaron A. Siegel|заглавие=Combinatorial Game Theory|издательство=AMS|год=2013|isbn=9780821851906|ref=Siegel}} |
* {{публикация|книга|автор=Aaron A. Siegel|заглавие=Combinatorial Game Theory|издательство=AMS|год=2013|isbn=9780821851906|ref=Siegel}} |
||
* {{публикация|книга |
* {{публикация|книга |
||
| Строка 253: | Строка 276: | ||
{{Внешние ссылки}} |
{{Внешние ссылки}} |
||
{{Conway's Game of Life|state=collapsed}} |
{{Conway's Game of Life|state=collapsed}} |
||
{{Избранная статья}} |
{{Избранная статья|Учёный|Математика}} |
||
[[Категория:Джон Конвей| ]] |
|||
[[Категория:Математики Великобритании]] |
[[Категория:Математики Великобритании]] |
||
[[Категория:Математики США]] |
[[Категория:Математики США]] |
||
| ⚫ | |||
[[Категория:Выпускники колледжа Гонвилл-энд-Киз]] |
[[Категория:Выпускники колледжа Гонвилл-энд-Киз]] |
||
[[Категория:Преподаватели Принстонского университета]] |
|||
[[Категория:Преподаватели Математического факультета Принстонского университета]] |
|||
| ⚫ | |||
[[Категория:Почётные доктора Ливерпульского университета]] |
|||
[[Категория:Умершие от COVID-19 в США]] |
|||
Текущая версия от 04:15, 14 ноября 2024
| Джон Хортон Конвей | |
|---|---|
| англ. John Horton Conway | |
 | |
| Дата рождения | 26 декабря 1937[1] |
| Место рождения | |
| Дата смерти | 11 апреля 2020[2][3][…] (82 года) |
| Место смерти | |
| Страна | |
| Род деятельности | математик, преподаватель университета |
| Научная сфера | теория групп, комбинаторная теория игр, математика[7], теория чисел[7], теория игр[7], теория узлов[7] и математические игры[вд][7] |
| Место работы | |
| Альма-матер |
|
| Научный руководитель | Гарольд Давенпорт |
| Награды и премии | |
Джон Хо́ртон Ко́нвей (англ. John Horton Conway; 26 декабря 1937 — 11 апреля 2020) — британский математик.
Известен в первую очередь как создатель игры «Жизнь». Однако его вклад в математику весьма многообразен и значителен. В теории групп он открыл группы Конвея и сформулировал гипотезу чудовищного вздора. Совместно с соавторами заложил основы комбинаторной теории игр, попутно открыв сюрреальные числа. Также внёс вклад в теорию узлов, теорию чисел. Многие работы Конвея лежат в области занимательной математики или близки к ней. В целом он был склонен исследовать красивые, наглядные объекты, такие как игры или многогранники, не заботясь о том, какое значение это имеет с точки зрения фундаментальной или прикладной науки.
Родился в Ливерпуле, Великобритания. Окончил Кембриджский университет, получил там же степень PhD в 1964 году и остался там же преподавать. На рубеже 1960—70-х годов стал известен как в профессиональном сообществе (благодаря группам Конвея), так и среди широкой публики (благодаря игре «Жизнь»). С 1986 года работал в Принстонском университете, США. Был ярким лектором; помимо преподавания в университетах, читал лекции и писал статьи о математике для школьников и широкой публики.
Биография
[править | править код]Семья, учёба
[править | править код]Отец Джона Хортона Конвея, Сирил, не окончил школу, но активно занимался самообразованием. У Сирила Конвея и его жены Агнес Бойс было трое детей: Джоан, Сильвия и младший Джон, родившийся в 1937 году в Ливерпуле[10]. Джон унаследовал от отца страсть к чтению и любовь к эффектным демонстрациям[11].
Джон Конвей был довольно замкнутым ребёнком, увлечённым математикой[12]. Идею своей нотации для узлов он задумал ещё подростком[13].
В 1956 году поступил в колледж Гонвилл-энд-Киз Кембриджского университета, причём решил вести себя там как экстраверт[12]. И действительно, в Кембридже он завёл друзей, вовлекался в разнообразную околоучебную и общественную деятельность. В частности, там он познакомился с Майклом Гаем, сыном математика Ричарда Гая; Майкл Гай стал лучшим другом Конвея и его соавтором по нескольким работам. Помимо прочего, в Кембридже Конвей с друзьями построили цифровой компьютер, работавший на водяных трубах и клапанах. Он проводил много времени за всевозможными играми и, в частности, играл с Абрамом Самойловичем Безиковичем в карточную игру «Свои козыри» в особой модификации Безиковича. Академическая успеваемость Конвея поначалу была на высоте, но затем ухудшилась[13].
В 1961 году женился на Эйлин Фрэнсис Хау[13]. У Эйлин образование в области иностранных языков: французский и итальянский[15]. У Джона и Эйлин родились четыре дочери в 1962—1968 годах: Сьюзан, Роуз, Елена и Энн-Луиза[10].
Начало научной и преподавательской карьеры
[править | править код]
Окончив колледж со степенью бакалавра в 1959 году[16], Джон Конвей стал аспирантом Гарольда Дэвенпорта. Тот сперва предложил для диссертации не слишком интересную задачу из области теории чисел о представлении целого числа в виде суммы пятых степеней. Конвей решил задачу, но не опубликовал эту свою работу. Позже решение опубликовал другой человек[13]. Конвей в итоге получил степень PhD в 1964 году, защитив диссертацию об одной немного более интересной, но тоже достаточно малозначительной задаче об ординалах[17].
Конвей получил позицию там же, в колледже Гонвилл-энд-Киз, на кафедре чистой математики. Он читал лекции, и они пользовались большой популярностью благодаря ярким и наглядным объяснениям, практически цирковым трюкам и импровизациям. У него часто не было плана и текста собственных лекций. Его студент Эндрю Гласс сделал подробный, упорядоченный конспект его лекций по абстрактным автоматам; этот конспект просили скопировать многие студенты, а потом и сам лектор, и спустя несколько лет этот конспект превратился в первую книгу Конвея, Regular algebra and finite machines[15].

Конвей много играл в математические игры с коллегами и студентами и регулярно придумывал их. Так, со студентом Майклом Патерсоном они изобрели топологическую игру рассада, которая немедленно приобрела на кафедре тотальную популярность. Конвей стал переписываться с Мартином Гарднером: об играх, включая рассаду, а также об алгоритме для решения разновидности задачи о справедливом дележе (открытом им независимо от более раннего решения Джона Селфриджа[20]). Кроме того, Конвей пытался визуально представить четырёхмерное пространство, и для этого он тренировал бинокулярное зрение с вертикальным параллаксом вместо горизонтального с помощью специального устройства. В этот же период он с коллегами исследовал последовательность «Посмотри-и-скажи»; как нередко случалось с его результатами, некоторые доказательства были неоднократно утеряны, найдены заново и в итоге опубликованы гораздо позже[15].
В целом в период после защиты диссертации жизнь Конвея шла приятно и беззаботно. Но он не занимался «серьёзной» математической работой, и это его угнетало[15].
Приход славы
[править | править код]Конец 1960-х и 1970-й годы выдались исключительно продуктивными для Конвея (он именовал этот период annus mirabilis[21]): он нашёл три новые спорадические группы, названные его именем, придумал правила игры «Жизнь» и построил сюрреальные числа.
Группы Конвея
[править | править код]В 1960-е годы активно шла работа по классификации простых конечных групп. Стало понятно, что может быть не открыто ещё несколько спорадических групп — простых конечных групп, не вписывающихся в общую классификацию. В это же время математик Джон Лич[англ.] нашёл чрезвычайно симметричную решётку, названную его именем, и он предположил, что в её группе симметрии может содержаться новая спорадическая группа. Британский математик Джон Маккей рассказал об этой задаче многим коллегам, в том числе математикам из Кембриджа Джону Томпсону и Джону Конвею. Томпсон уже тогда был признанным корифеем теории групп (и чрезвычайно заняты́м человеком), Конвей же лишь обладал некоторыми знаниями в этой области. Томпсон предложил Конвею вычислить порядок группы симметрии решётки Лича. Тот решил взяться за эту задачу и приготовился заниматься ею по 6—12 часов дважды в неделю в течение нескольких месяцев[22][23].
В первый назначенный день исследования решётки Лича Конвей, по его словам, «поцеловал жену и детей на прощанье» и принялся за работу. И уже к вечеру этого дня он смог не только вычислить порядок группы, но и построить её и найти содержащиеся в ней три новые спорадические группы[23]. За этим последовали дискуссии с Томпсоном, публикация результатов в статье 1968 года, путешествия по конференциям и семинарам по всему миру с докладами о найденных группах. С этого момента Джон Конвей смог больше не беспокоиться о том, достаточно ли серьёзной математикой он занимается[22].
Игра «Жизнь»
[править | править код]Конвей интересовался темой клеточных автоматов и, в частности, автоматом фон Неймана ещё с детства. Он поставил целью придумать как можно более простой клеточный автомат с нетривиальным, непредсказуемым поведением, надеясь, что в таком случае он будет тьюринг-полным. Команда энтузиастов (Конвей, его коллеги и студенты) занималась перебором бесчисленных вариаций правил в поисках подходящих. Их усилия были вознаграждены, когда они придумали то, что стало известно как игра «Жизнь». Конвей изложил основные сведения об игре «Жизнь», которые удалось выяснить, в письме к Мартину Гарднеру 1970 года. Тот написал об игре «Жизнь» в своей колонке в журнале Scientific American, и эта заметка стала самой популярной из всех, вышедших в этой колонке. Игра «Жизнь» получила тысячи поклонников по всей Америке и за её пределами, а её изобретатель приобрёл известность среди широкой публики[25].
Вскоре Конвей доказал тьюринг-полноту игры «Жизнь» (доказательство не было опубликовано). После этого он практически потерял интерес к этой теме. Он был недоволен тем, насколько игра «Жизнь» более известна, чем другие его работы, и не слишком любил о ней рассказывать — кроме как отдельным интересующимся детям[26][27].
Сюрреальные числа и книги об играх
[править | править код]Годы изобретения и обдумывания игр не прошли даром. Ричард Гай развил теорию, описывающую широкий класс игр, и когда во второй половине 1960-х годов он и американский математик Элвин Берлекэмп задумали книгу об играх, они пригласили Конвея стать их соавтором[28]. Пока шла работа над книгой, получившей название Winning Ways for Your Mathematical Plays, Конвей продолжал исследовать игры и обнаружил, что позиции в так называемых пристрастных играх могут быть выражены числами, причём класс необходимых для этого чисел включает не только целые и действительные числа, но и некоторые новые числа. Дональд Кнут назвал эти числа сюрреальными. Конвей считал сюрреальные числа своим главным поводом для гордости[21][29].
Хотя теория пристрастных игр вошла в Winning Ways, она получила там не очень подробное освещение, особенно в части, касающейся сюрреальных чисел. Об этих числах Конвей написал Гарднеру в том же письме 1970 года, в котором сообщил об игре «Жизнь», а позже, в 1976 году, он быстро написал и выпустил собственную книгу On Numbers and Games о пристрастных играх и сюрреальных числах. Когда он сообщил об этом Берлекэмпу, тот был крайне недоволен и едва не рассорился с кембриджским соавтором, и только Гай смог помирить их. Winning Ways в итоге была дописана только в 1981 году; на следующий год книга вышла и стала бестселлером (несмотря на отсутствие рекламы от издательства), так же как и On Numbers and Games до того[21][29].
Эти две книги об играх, как и многие другие работы Конвея, несут явственный отпечаток его любви к неортодоксальной терминологии и каламбурам[21]: так, например, числа с чётным и нечётным количеством единиц в двоичной записи именуются, соответственно, злыми и одиозными — англ. evil и odious, ср. с even и odd (с англ. — «чётные» и «нечётные»)[30].
Работа над Атласом
[править | править код]В начале 1970-х годов Джон Конвей задумал составить справочник по конечным группам. Эту будущую книгу назвали «Атласом конечных групп» — Atlas of the Finite Groups. В проекте приняли участие аспиранты Конвея Роберт Кёртис, Саймон Нортон и Роберт Уилсон, а также Ричард Паркер. Они собрали и перепроверили множество данных по конечным группам и в итоге приняли решение включить в Атлас в первую очередь таблицы характеров. Работа растянулась на много лет[JHC 1][32].
В 1970-е годы сообщество продолжало очень активно разрабатывать классификацию простых конечных групп, и Конвей продолжал работать над спорадическими группами. В частности, он поучаствовал в определении размера монстра (и придумал это название для группы). К 1978 году другими специалистами по теории групп были вычислены таблицы характеров монстра (построена эта группа, однако, ещё не была). И в этот момент Джон Маккей заметил, что размерность одного из представлений монстра, 196883, лишь на единицу отличается от линейного коэффициента фурье-разложения j-инварианта — одной модулярной функции, равного 196884. Конвей и Нортон собрали это и другие наблюдения от разных авторов и сформулировали гипотезу о глубокой связи между модулярными функциями и конечными группами, назвав её «гипотезой чудовищного вздора»[34] — англ. monstrous moonshine: прилагательное отсылает к монстру, а moonshine переводится не только как «вздор», но также как «самогон» и «лунный свет»; все эти смыслы означают, что гипотеза неожиданная, сбивающая с толку, удивительная и ускользающая[32].
Кроме того, тогда же, в середине 1970-х, Конвей занимался книгами об играх и мозаикой Пенроуза. В этот же период Гарднер показал ему заметку Льюиса Кэрролла в Nature 1887 года с описанием алгоритма для быстрого определения дня недели, на который приходится заданная дата, и предложил придумать алгоритм, который был бы ещё проще для вычисления и запоминания. В результате Конвей составил алгоритм Судного дня, который стал его увлечением и одним из любимых трюков: он десятилетиями оттачивал алгоритм, мнемоники для его запоминания и свой собственный навык его использования[32].

В конце 1970-х годов Конвей расстался с Эйлин и встретил Ларису Куин. Лариса приехала из Волгограда (СССР)[35] и была его аспиранткой[36], занималась исследованием гипотезы чудовищного вздора; она получила степень PhD в Кембридже в 1981 году[37]. Джон и Лариса поженились в 1983 году, когда у них родился сын Алекс (на кафедре его прозвали малым монстром в честь группы). В 1983 году Конвей получил должность полного профессора. В первой половине 1980-х годов аспирантом Конвея стал Ричард Борчердс, который позже доказал гипотезу чудовищого вздора[38].
Между тем в 1984 году Атлас наконец был завершён. Ещё год ушёл на подготовку его к печати. Его публикация стала долгожданным событием для работавших в области теории групп математиков по всему миру[38][JHC 1].
Принстон
[править | править код]1986—1987 учебный год Джон Конвей провёл в Принстонском университете (США), временно занимая по приглашению тогдашнего главы кафедры математики Элиаса Стайна только что учреждённую[39] позицию Фоннеймановского профессора прикладной и вычислительной математики. Конвею было предложено остаться на этой должности на постоянной основе. Он сильно колебался, но в итоге мнение жены, бо́льшая зарплата, уход из Кембриджа многих коллег-математиков и общее желание перемен склонили его принять предложение[38].

В Принстоне Конвей тоже прославился харизмой и эксцентричностью. Преподавание поначалу шло не слишком успешно: ему предлагали скучную и бессодержательную тему для курса лекций, а когда он сам решил прочитать курс лекций о монстре, оказалось, что этот курс не пользовался большой популярностью среди студентов, но привлёк в аудиторию некоторых профессоров, что мешало. Но дела пошли на лад, когда он стал сотрудничать со знаменитым топологом Уильямом Тёрстоном. Конвей и Тёрстон придумали курс «Геометрия и воображение», к ним присоединились преподаватели Питер Дойл и Джейн Гилман. На лекциях этого курса царила живая атмосфера, в качестве наглядных иллюстраций математических концепций использовались фонарики, велосипеды, LEGO и Конвеев живот. Кроме того, Тёрстон познакомил Конвея со своей идеей орбифолдного подхода к группам симметрии двумерного пространства, который тот затем развил. В целом в Принстоне Конвей стал больше педагогом, чем исследователем[40].

Время от времени Конвей, рассказывая на различных выступлениях о тех или иных интересных нерешённых задачах, предлагал денежные призы за их решение. Размер приза соответствовал предполагаемой сложности задачи, и обычно он был сравнительно небольшой. Конвей дружил с Нилом Слоуном, автором «Энциклопедии целочисленных последовательностей», и неудивительно, что многие из этих задач были связаны с целочисленными последовательностями. В 1988 году произошла история с последовательностью, которая теперь известна как 10000-долларовая последовательность Хофштадтера — Конвея. Конвей намеревался предложить 1000 долларов за доказательство определённого утверждения об асимптотическом поведении последовательности, но, оговорившись, назвал в 10 раз большую сумму — весьма существенную для своего бюджета; при этом задача оказалась легче, чем предполагалось, и уже через две недели статистик Колин Мэллоуз решил её (с несущественной ошибкой, как позже оказалось). Узнав об оговорке Конвея, Мэллоуз отказался обналичивать присланный им чек, Конвей же настаивал на принятии приза; договорились они в итоге на 1000 долларов[40].
В 1988 году в семье Джона и Ларисы родился сын Оливер (впоследствии оба их сына стали заниматься точными науками, следуя по стопам родителей). В 1992 году они пережили тяжёлый развод. Следствием этого для Конвея стали финансовые трудности и недостаток общения с сыновьями. У него случился инфаркт, на следующий год — ещё один. На фоне этих проблем предпринял попытку самоубийства, устроив себе передозировку лекарств. Восстановиться после этого физически и психологически ему помогли друзья, в первую очередь Нил Слоун[40].
Поздние годы
[править | править код]Конвей и его третья жена, Диана Катсоуджордж[36], впервые встретились в 1996 году; она тогда работала в университетском книжном магазине[42]. Они поженились в 2001 году (и мирно разошлись через несколько лет, впоследствии активно общались[43]), тогда же у них родился сын Гарет[10].
Конвей регулярно читал публичные популярные лекции на разнообразные темы, связанные с математикой, и с 1998 года преподавал в математических лагерях для школьников, таких как Canada/USA Mathcamp[44][45].
В 2004 году Конвей и канадский математик Саймон Кошен доказали так называемую теорему о свободе воли; ещё некоторое время заняла подготовка публикации, и затем в течение нескольких лет соавторы теоремы развивали свой результат и обсуждали его с сообществом[12].
Конвей ушёл на должность эмерит-профессора в 2013 году[16]. В первые годы после формальной отставки он продолжил работать едва ли не активнее, чем до неё — выступать на конференциях, выпускать новые работы, преподавать в математических лагерях для школьников[12][47]. В 2018 году он пережил обширный инсульт[48]. Скончался в Нью-Брансуике 11 апреля 2020 года в возрасте 82 лет от осложнений на фоне коронавирусной инфекции COVID-19[42].
Личность
[править | править код]
По свидетельствам людей, знавших Конвея, он был харизматичным и дружелюбным, при этом обладал значительным самомнением, что сам охотно признавал[49]. Рассказывая о себе, нередко противоречил своим и чужим словам[11]. Бытовыми сторонами жизни он пренебрегал, исключительно небрежно относился к полученным письмам и другим документам[49]. Хотя в целом вёл себя расслабленно, в периоды исследования математической задачи он работал много, интенсивно и дотошно[21]. Математика была единственным интересом Конвея, при этом математические аспекты он замечал везде — не только в играх, но и в, казалось бы, бытовых предметах[38]. С юности проявлял пацифистские взгляды[13], подписывал разнообразные политические петиции[22], хотя и не участвовал в политике активно. Был любвеобилен, не соблюдал верность своим жёнам, что и становилось одной из важных причин, по которой они расставались с ним[21]. Атеист[50].
Научный вклад
[править | править код]Джон Хортон Конвей говорил, что не проработал ни дня в своей жизни, а лишь всегда играл в игры[49].
Теория групп и близкие области
[править | править код]Конвей был склонен подходить к исследованиям математических объектов, в том числе групп, с геометрической точки зрения, визуально представляя себе связанные с ними симметрии[51], и вообще очень ценил наглядность и красоту математических теорий[38]. Кроме того, он предпочитал необычные частные случаи общим. Эти особенности стиля и склонностей Конвея ярко проявились в его работах по теории групп[51].
Спорадические группы
[править | править код]
Одно из самых важных достижений Конвея — исследование группы автоморфизмов решётки Лича Co0. Он нашёл, что эта группа имеет порядок 8 315 553 613 086 720 000 и включает три новые спорадические группы Co1, Co2, Co3 (их простота была впервые показана Джоном Томпсоном; Co0 включает и некоторые другие спорадические группы, открытые незадолго до того[52]): Co1 — факторгруппа Co0 по её центру, единственным нетривиальным элементом которого является домножение на −1, Co2 и Co3 — подгруппы Co0, стабилизаторы определённых векторов решётки. Эти группы вместе называют группами Конвея[53][JHC 2][JHC 3].
Он исследовал и другие спорадические группы. В частности, вместе с Дэвидом Уэльсом впервые разработал построение группы Рудвалиса Ru[54][JHC 4]. Также вместе с различными соавторами упростил построение различных групп, которые были построены или предсказаны другими авторами, например, ввёл построение группы Фишера Fi22 через 77-мерное представление над полем из трёх элементов[55].
Чудовищный вздор
[править | править код]Особенное значение имеет работа Конвея над монстром, проделанная в период, когда существование этой группы ещё не было доказано, но о её свойствах уже было многое известно.
Джон Маккей и другие авторы сделали ряд наблюдений о структуре монстра и некоторых других групп и определённых численных совпадениях, в частности, о том, что коэффициенты фурье-разложения модулярной функции j-инварианта представляются простыми линейными комбинациями размерностей представлений монстра. Джон Томпсон предложил рассмотреть степенные ряды с коэффициентами, являющимися характерами представлений монстра, вычисленными для различных его элементов. Конвей и Саймон Нортон развили эти наблюдения, построили такие функции (ряды Маккея — Томпсона) и обнаружили, что они похожи на модулярные функции особого вида, известные как нем. Hauptmodul. Они сформулировали гипотезу, что каждый ряд Маккея — Томпсона действительно соответствует определённому Hauptmodul, что подразумевало глубокую и загадочную связь между спорадическими группами и модулярными функциями. Эта гипотеза получила название «гипотеза чудовищного вздора» — англ. monstrous moonshine[56][JHC 5].
Гипотезу Конвея и Нортона доказал Ричард Борчердс с помощью алгебр вершинных операторов. Однако сам Конвей и другие специалисты считали, что работа Борчердса хотя и формально доказывает гипотезу, но не объясняет её. Обнаруженные связи между алгебраическими объектами, такими как группы, и понятиями, связанными с модулярными функциями, были затем развиты и обобщены. Кроме того, оказалось, что эти связи могут быть сформулированы естественным образом на языке конформных теорий поля. Все вместе эти наблюдения, гипотезы и теоремы называют просто «вздор» — moonshine. В этой области ещё много открытых задач и неотвеченных вопросов[56][57].
Помимо конечных групп, Конвей исследовал также решётки и упаковки сфер, а также близкую тему кодов коррекции ошибок[JHC 6]. В частности, он разработал новое построение для той же решётки Лича[58]. Конвей и Нил Слоун изложили свои результаты и большое количество справочной информации в своей книге Sphere Packings, Lattices, and Groups.

Решётки, в свою очередь, связаны с темой кристаллографических групп и замощений.
В этой области важное достижение Конвея — популяризация и развитие придуманного Уильямом Тёрстоном подхода к изучению периодических групп симметрии евклидова, сферического и гиперболического пространств. Этот подход имеет топологическую природу и основан на орбифолдах[40]. Орбифолд — это топологическое пространство, снабжённое определённой структурой, связанной с действием на него заданной конечной группы. Двумерные параболические орбифолды (те, у которых аналог эйлеровой характеристики равен нулю) напрямую соответствуют двумерным кристаллографическим группам[59]. На этом основана придуманная Конвеем и достаточно широко распространившаяся орбифолдная нотация[англ.] для этих и других подобных групп[60][JHC 7]. Орбифолды связаны и с чудовищным вздором[61].
Известен критерий Конвея для плиток, замощающих плоскость.
Тема замощений сферы непосредственно связана с многогранниками. Конвей придумал нотацию для многогранников[62] — ещё один пример его большой любви к изобретению и переизобретению названий и нотаций[40]. Кроме того, Конвей и Майкл Гай перечислили все четырёхмерные архимедовы тела и открыли великую антипризму[англ.] — единственный невитхоффов однородный политоп[13][16][JHC 8].
Атлас
[править | править код]Конвей известен как руководитель группы, собравшей «Атлас конечных групп» — грандиозный справочник, содержащий таблицы характеров конечных групп (не только спорадических) и ставший ценным инструментом для математиков, работавших с конечными группами в эпоху до развития интернета[32]. Сейчас Атлас существует в виде интернет-энциклопедии, сделанной командой под руководством Роберта Уилсона[63].
Вклад Конвея в комбинаторную теорию игр — одно из самых известных его достижений[16].
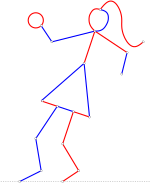
Конвей изобрёл множество игр, в том числе, например, рассаду (англ. Sprouts, совместно с Майклом Патерсоном), фатбол и хакенбуш[англ.]. Ричард Гай, в свою очередь, развил систематическую теорию беспристрастных игр (англ. impartial games) на основе функции Шпрага — Гранди. Конвей же, основываясь на идее сложения игр, смог заложить теорию для более широкого класса игр — пристрастных игр[англ.] (англ. partizan games) — игр, в которых в одной и той же позиции разным игрокам доступны разные ходы (например, в шахматах или го каждый игрок может ходить только фигурами или камнями своего цвета). Гай, Конвей и Элвин Берлекэмп изложили общую теорию, результаты по многим конкретным играм и различные открытые задачи (такие как Задача об Ангеле и Дьяволе) в книге Winning Ways for Your Mathematical Plays[21][29].
Исследуя пристрастные игры и включив в рассмотрение трансфинитные игры, Конвей обнаружил, что для описания позиций в таких играх нужен новый класс чисел, включающий и целые, и действительные числа, и ординалы (например, и ), и другие, новые числа (например, , и ), которые строятся при помощи конструкции, похожей на дедекиндово сечение. Эти числа получили название сюрреальных. Результаты своих исследований пристрастных игр и сюрреальных чисел Конвей подробно изложил в книге On Numbers And Games. Книги Winning Ways и On Numbers And Games вместе заложили основу комбинаторной теории игр как организованной и плодотворной математической дисциплины[21][29].
Сюрреальные числа привлекают многих своим разнообразием и естественностью. Однако применений за пределами комбинаторной теории игр им практически не нашлось, хотя в этом направлении предпринимались определённые усилия. Так, сам Конвей (безуспешно) обсуждал с Гёделем возможность использования сюрреальных чисел для построения «правильной теории бесконечно малых», а Мартин Крускал вложил много сил в развитие сюрреального анализа в надежде использовать его в теоретической физике[21][40].
Добавим ещё, что Конвей — один из открывателей алгоритма Селфриджа — Конвея для решения разновидности задачи о справедливом дележе для трёх участников, которая относится к более широкой области — теории игр[20].

Джон Конвей придумал игру «Жизнь» — известный клеточный автомат. Он определён на поле, замощённом квадратами. Каждая клетка поля в каждый момент (дискретного) времени считается живой либо мёртвой, причём на следующем временно́м шаге состояние клетки определяется следующими правилами, зависящими от состояния её восьми клеток-соседей на текущем шаге[49]:
- если клетка была живой, то она остаётся живой, если у неё было ровно 2 или 3 живых соседа;
- если клетка была мёртвой, то она становится живой, если у неё было ровно 3 живых соседа.
Игра «Жизнь» не является игрой в обычном смысле, в ней нет состязающихся игроков, «игра» состоит лишь в подборе начальной конфигурации клеток и наблюдении за их развитием[49].
Конвей подобрал правила игры «Жизнь» так, что начальные конфигурации даже из небольшого количества клеток развиваются зачастую совершенно непредсказуемо. Как затем оказалось, на поле игры «Жизнь» могут существовать неподвижные, стабильно перемещающиеся, стабильно размножающиеся конфигурации, логические вентили, позволяющие реализовать в ней произвольное вычисление (полнота по Тьюрингу), и многие другие нетривиальные конструкции. Возможно множество вариантов и обобщений игры «Жизнь»[64].
Появление игры «Жизнь» привело к огромному росту интереса к клеточным автоматам[49]. Клеточные автоматы, подобные игре «Жизнь», стали инструментом моделирования природных процессов[65][66], способом генерации красивых изображений[67] и популярным упражнением по программированию[68].
Вокруг игры «Жизнь» сразу сложилось сообщество энтузиастов-исследователей[26]. Такое сообщество существует и сейчас, обмениваясь информацией о новых открытиях на сайте ConwayLife.com[69].
Среди клеточных автоматов несколько другого типа, придуманных в непосредственном окружении Конвея, можно также отметить червей Патерсона[70].
Конвей изобрёл тьюринг-полный эзотерический язык программирования FRACTRAN. Программа на этом языке представляет собой упорядоченный набор обыкновенных дробей и стартовое целое число. Чтобы выполнить программу, нужно последовательно умножать имеющееся целое число на первую такую дробь из набора, что в результате вновь получается целое число (тем самым возникающие целые числа формируют последовательность), до тех пор, пока это возможно[JHC 9]. Так, Конвей приводит программу для генерации простых чисел:
При стартовом числе 2 в последовательности, получающейся при выполнении программы, будут время от времени возникать другие степени двойки, и показатели этих степеней образуют в точности последовательность простых чисел[25].
Используя FRACTRAN, он показал, что некоторые аналоги гипотезы Коллатца неразрешимы[71][JHC 10].
Прямое отношение к тематике решёток, которой Конвей тоже занимался, имеют целочисленные квадратичные формы. О них он вместе со своим студентом Уильямом Шнибергером сформулировал утверждения[англ.], согласно которым:
- положительно определённая квадратичная форма с целочисленной матрицей представляет все натуральные числа тогда и только тогда, когда она представляет все натуральные числа, меньшие либо равные 15;
- положительно определённая квадратичная форма с целочисленными значениями представляет все натуральные числа тогда и только тогда, когда она представляет все натуральные числа, меньшие либо равные 290.
Эти утверждения родственны теореме Лагранжа о сумме четырёх квадратов (как и несостоявшаяся первая диссертация Конвея). Конвей и Шнибергер доказали первое утверждение, но доказательство было сложным, и было опубликовано лишь в виде наброска в диссертации Шнибергера. Впоследствии Манджул Бхаргава упростил доказательство первой теоремы, обобщил её и доказал вторую теорему совместно с Дж. Ханке[72][JHC 11].
Конвей придумал стрелочные обозначения для очень больших чисел[16].
Также он проанализировал последовательность «Посмотри-и-скажи»: составил таблицу отдельно эволюционирующих «элементов» членов последовательности и получил универсальный множитель, на который в среднем увеличивается длина члена последовательности независимо от начальной строки цифр. Этот множитель называют постоянной Конвея, и он представляет собой алгебраическое число 71-й степени[15][JHC 12].

Развив идеи Томаса Киркмана[англ.], Конвей разработал нотацию для узлов и зацеплений, основанную на вставке определённых плетений[англ.] в вершины некоторых 4-регулярных планарных графов. Это позволило ему быстро и легко воспроизвести существовавшие таблицы узлов с небольшим числом пересечений и исправить большинство из ошибок этих таблиц[73][74][JHC 13].
Кроме того, он разработал свой вариант многочлена Александера — полиномиального инварианта узлов — и обратил внимание на важность скейн-соотношений, которые затем стали распространённым удобным способом определения полиномиальных инвариантов узлов[75].
Конвей нашёл названный в честь него узел с 11 пересечениями, примечательный тем, что некоторые вопросы теории узлов применительно к нему оказываются особенно сложными[76].
Совместно с Саймоном Кошеном Конвей доказал теорему о свободе воли. Теорема опирается на несколько базовых постулатов квантовой теории. Согласно теореме, если у экспериментаторов есть свобода воли, то она есть и у элементарных частиц. Под намеренно провокационным термином «свобода воли» понимается спонтанное поведение, которое принципиально не определяется заранее. Тем самым теорема отвергает теории скрытых параметров и детерминизм. Многие физики сочли, что теорема не привносит ничего существенно нового, но в философии она вызвала заметное обсуждение[77][78][JHC 14].
Конвей тратил значительное время на занятия, которые многие сочли бы бесполезной тратой усилий[49]. Возможно, самый характерный пример — изобретённый им алгоритм Судного дня для определения дня недели для заданной даты. Конвей потратил очень много времени как на упрощение алгоритма, так и на тренировку своего навыка его использования[32][77]. Он интересовался и хорошо изученными областями, в которых трудно получить новый результат, такими как геометрия треугольника — так, он упростил доказательство теоремы Морли[40]. Не чуждался и головоломок — известна головоломка Конвея. Изучение разнообразных числовых последовательностей тоже зачастую ближе к занимательной математике, чем к реальной науке — хотя, к примеру, результаты о последовательностях типа фигурирующей в гипотезе Коллатца действительно нетривиальны и представляют общий интерес, это едва ли можно сказать о таких исследованных Конвеем известных последовательностях, как RATS и subprime Fibonacci[79]. Интересы Конвея простирались и в такие темы, как еврейский календарь и этимология необычных английских слов[16]. Разграничить глубокую научную работу и легкомысленные развлечения в деятельности Конвея зачастую невозможно[80]. Довольно запутан в этом отношении и статус некоторых его известных работ, упомянутых выше (это связано и с тем, что его самого этот вопрос не заботил): комбинаторная теория игр изначально воспринималась в основном как развлечение и лишь со временем приобрела более веский статус[29], а клеточные автоматы значительная часть научного сообщества всегда воспринимала как область занимательной математики без какого-либо глубокого теоретического значения[81].
Научное руководство
[править | править код]Степень PhD под руководством Конвея получили более двух десятков аспирантов, включая будущего филдсовского лауреата Ричарда Борчердса[82].
Признание
[править | править код]
- Премия Бервика[англ.] (1971)[84]
- Избран членом Лондонского королевского общества (1981)[85]
- Премия Пойа[англ.] (1987)[84]
- Избран членом Американской академии искусств и наук (1992)[86]
- Премия Неммерса по математике (1998)[87]
- Премия Стила (2000)[88]
- Премия Джозефа Пристли (2000-01)[89]
- Многочисленные почётные научные степени[47]
В 2015 году вышла биография Конвея — книга Шивон Робертс «Genius at Play: The Curious Mind of John Horton Conway» (Roberts, 2015)[27][90].
Библиография
[править | править код]Библиография Конвея включает около 100 статей в научных журналах, несколько десятков статей в научно-популярных изданиях и трудах конференций и 9 книг. Список публикаций в научных математических изданиях за всё время и список публикаций во всех научных изданиях приблизительно с начала 1970-х годов имеются в базах данных zbMATH и Scopus, соответственно. Полный список публикаций за период до 1999 года доступен на сайте Принстонского университета[91]. Избранная библиография приведена в книге Roberts, 2015.
Книги
[править | править код]- J. H. Conway. Regular Algebra and Finite Machines. — London : Chapman and Hall, 1971. — ISBN 9780412106200.
- Репринт: J. H. Conway. Regular Algebra and Finite Machines. — New York : Dover, 2012. — ISBN 9780486310589. — ISBN 9780486485836.
- J. H. Conway. On Numbers and Games. — New York : Academic Press, 1976. — ISBN 9780121863500.
- Второе издание: J. H. Conway. On Numbers and Games. — 2nd ed. — Wellesley, Massachusetts : A K Peters, 2001. — ISBN 9781568811277.
- Elwyn R. Berlekamp, John Horton Conway, Richard K. Guy. Winning Ways for Your Mathematical Plays. — Academic Press, 1982. — ISBN 9780120911509 (vol. 1). — ISBN 9780120911028 (vol. 2).
- Второе издание: Elwyn R. Berlekamp, John Horton Conway, Richard K. Guy. Winning Ways for Your Mathematical Plays. — 2nd ed. — Wellesley, Massachusetts : A K Peters, 2001—2004. — ISBN 9781568811307 (vol. 1). — ISBN 9781568811420 (vol. 2). — ISBN 9781568811437 (vol. 3). — ISBN 9781568811444 (vol. 4).
- J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker, R. A. Wilson. Atlas of Finite Groups. — Clarendon Press, 1985. — ISBN 9780198531999.
- J. H. Conway, N. J. A. Sloane. Sphere Packings, Lattices, and Groups. — New York : Springer-Verlag, 1988. — ISBN 9780387966175.
- Русский перевод первого издания: Конвей Дж., Слоэн Н. Упаковки шаров, решётки и группы. — М. : Мир, 1990. — ISBN 9785030023687 (том 1). — ISBN 9785030023694 (том 2).
- Третье издание: J. H. Conway, N. J. A. Sloane. Sphere Packings, Lattices, and Groups. — 3rd ed. — New York : Springer-Verlag, 1999. — Errata. — ISBN 9781475720167. — ISBN 9781475720167.
- J. H. Conway, Richard K. Guy. The Book of Numbers. — New York : Springer-Verlag, 1996. — ISBN 0614971667.
- J. H. Conway assisted by Francis Y. C. Fung. The Sensual (Quadratic) Form. — MAA, 1997. — ISBN 9780883850305.
- Русский перевод: Конвей Дж. Квадратичные формы, данные нам в ощущениях. — М. : МЦНМО, 2008. — ISBN 9785940572688.
- John H. Conway, Derek A. Smith. On Quaternions and Octonions : Their geometry, arithmetic, and symmetry. — Taylor & Francis, 2003. — Errata. — ISBN 9781439864180.
- Русский перевод: Конвей Дж., Смит Д. О кватернионах и октавах, об их геометрии, арифметике и симметриях. — М. : МЦНМО, 2009. — ISBN 9785940575177.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. The Symmetries of Things. — Taylor & Francis, 2008. — Errata. — ISBN 9781568812205.
Некоторые статьи
[править | править код]Избранные статьи Конвея опубликованы на русском языке в сборнике «Человек, который играл в математику».
- ↑ 1 2 John H. Conway, Robert T. Curtis and Robert A. Wilson. A brief history of the Atlas // The Atlas of Finite Groups: Ten Years on. — Cambridge University Press, 1998. — ISBN 0521575877.
- ↑ J. H. Conway. A Perfect Group of Order 8,315,553,613,086,720,000 and the Sporadic Simple Groups // Bull. London Math. Soc. — 1969. — Vol. 1. — P. 79—88. — doi:10.1112/blms/1.1.79.
- ↑ J. H. Conway. A Group of Order 8,315,553,613,086,720,000 // PNAS. — 1968. — Vol. 61. — P. 398—400. — doi:10.1073/pnas.61.2.398.
- ↑ J. H. Conway and D. B. Wales. The construction of the Rudvalis simple group of order 145,926,144,000 // Journal of Algebra. — 1973. — Vol. 27. — P. 538—548. — doi:10.1016/0021-8693(73)90063-X.
- ↑ J. H. Conway and S. P. Norton. Monstrous Moonshine // Bull. London Math. Soc. — 1979. — Vol. 11. — P. 308—339. — doi:10.1112/blms/11.3.308.
- ↑ J. H. Conway, R. H. Hardin and N. J. A. Sloane. Packing Lines, Planes, etc.: Packings in Grassmannian Spaces // Experimental Mathematics. — 1996. — Vol. 5. — P. 139—159. — doi:10.1080/10586458.1996.10504585.
- ↑ J. H. Conway and D. H. Hudson. The Orbifold Notation for Two-Dimensional Groups // Structural Chemistry. — 2002. — Vol. 13. — P. 247—257. — doi:10.1023/A:1015851621002.
- ↑ J. H. Conway and M. J. T. Guy. Four-Dimensional Archimedean Polytopes // Proceedings of the Colloquium on Convexity at Copenhagen. — 1965. — P. 38—39.
- ↑ J. H. Conway. Фрактран: простой универсальный язык программирования для арифметики : [арх. 20 мая 2023] = FRACTRAN: A Simple Universal Programming Language for Arithmetic // Open Problems Commun. Comput. — 1987. — P. 4—26. — doi:10.1007/978-1-4612-4808-8_2.
- ↑ J. H. Conway. On Unsettleable Arithmetical Problems // Amer. Math. Monthly. — 2013. — Vol. 120. — P. 192—198. — doi:10.4169/amer.math.monthly.120.03.192.
- ↑ J. H. Conway. Universal quadratic forms and the fifteen theorem // Quadratic Forms and Their Applications. — 2000. — P. 23—26. — (Contemp. Math.). — doi:10.1090/conm/272/04394.
- ↑ J. H. Conway. The Weird and Wonderful Chemistry of Audioactive Decay // Open Problems Commun. Comput. — 1987. — P. 173—188. — doi:10.1007/978-1-4612-4808-8_53.
- ↑ J. H. Conway. An Enumeration of Knots and Links, and Some of Their Algebraic Properties // Computational Problems in Abstract Algebra. — 1970. — P. 329—358. — doi:10.1016/B978-0-08-012975-4.50034-5.
- ↑ J. H. Conway and S. Kochen. The Free Will Theorem // Foundations of Physics. — 2006. — Vol. 36. — P. 1441—1473. — arXiv:quant-ph/0604079. — doi:10.1007/s10701-006-9068-6.
Примечания
[править | править код]- ↑ Архив по истории математики Мактьютор — 1994.
- ↑ Lum P. Mathematician John Horton Conway has died after contracting Covid-19 (англ.) — 2020.
- ↑ Воронцов Н. Создатель игры «Жизнь» математик Джон Конвей умер от COVID-19 — 2020.
- ↑ Zandonella C. Mathematician John Horton Conway, a ‘magical genius’ known for inventing the ‘Game of Life,’ dies at age 82 (англ.) — Princeton University, 2020.
- ↑ Roberts S. John Horton Conway, a ‘Magical Genius’ in Math, Dies at 82 (англ.) — The New York Times, 2020.
- ↑ LIBRIS — Национальная библиотека Швеции, 2012.
- ↑ 1 2 3 4 5 Чешская национальная авторитетная база данных
- ↑ John Horton Conway. Curriculum Vitae
- ↑ E-Theses Online Service
- ↑ 1 2 3 Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Конвей, Джон Хортон (англ.) — биография в архиве MacTutor.
- ↑ 1 2 Roberts, 2015, 2. Dazzling New World.
- ↑ 1 2 3 4 Roberts, 2015, 1. Identity Elements.
- ↑ 1 2 3 4 5 6 Roberts, 2015, 3. Gymnastics.
- ↑ Siobhan Roberts. This Early Computer Was Based on a Urinal Flush Mechanism. Nautilus (30 июня 2015). Дата обращения: 28 июля 2023. Архивировано 7 июня 2023 года.
- ↑ 1 2 3 4 5 Roberts, 2015, 5. Nerdish Delights.
- ↑ 1 2 3 4 5 6 John Horton Conway. Princeton University. Дата обращения: 24 апреля 2023. Архивировано 24 апреля 2023 года.
- ↑ Roberts, 2015, 4. Calculate the Stars.
- ↑ Siobhan Roberts. Inside the mind of ‘mathemagician’ John Horton Conway. The Toronto Star (23 августа 2015). Дата обращения: 12 сентября 2023. Архивировано 12 сентября 2023 года.
- ↑ Siobhan Roberts, John Horton Conway. John Conway. Genius Behind The Numbers. 52 Insights (7 января 2016). Дата обращения: 11 марта 2023. Архивировано 11 марта 2023 года.
- ↑ 1 2 Steven J. Brams and Alan D. Taylor. Fair Division. From cake-cutting to dispute resolution. — Cambridge University Press, 1996. — P. 116. — ISBN 0521556449.
- ↑ 1 2 3 4 5 6 7 8 9 Roberts, 2015, 10. Snip, Clip, Prune, Lop.
- ↑ 1 2 3 Roberts, 2015, 6. The Vow.
- ↑ 1 2 Thompson, 1984, pp. 118—123.
- ↑ 1 2 3 Siobhan Roberts. A Life in Games. Quanta (28 августа 2015). Дата обращения: 9 марта 2019. Архивировано 19 апреля 2019 года.
- ↑ 1 2 Roberts, 2015, 8. Criteria of Virtue.
- ↑ 1 2 Roberts, 2015, 9. Character Assassination.
- ↑ 1 2 Joseph O’Rourke. Book Review. Genius at Play: The Curious Mind of John Horton Conway by Siobhan Roberts // The College Mathematics Journal. — 2015. — Vol. 46, no. 4. — P. 309—314. — doi:10.4169/college.math.j.46.4.309.
- ↑ Donald J. Albers, Gerald L. Alexanderson, eds. Fascinating Mathematical People: Interviews and Memoirs. — Princeton University Press, 2011. — P. 175. — ISBN 9781400839551.
- ↑ 1 2 3 4 5 Siegel, 2013, A Finite Loopfree History.
- ↑ J.-P. Allouche, Benoit Cloitre and V. Shevelev. Beyond odious and evil // Aequationes Mathematicae. — 2016. — Vol. 90. — P. 341—353. — arXiv:1405.6214. — doi:10.1007/s00010-015-0345-3.
- ↑ Siobhan Roberts. 7 Facts About the Charming "God-Monster" Mathematical Iconoclast John Horton Conway. Biography (13 декабря 2015). Дата обращения: 16 марта 2019. Архивировано из оригинала 4 января 2016 года.
- ↑ 1 2 3 4 5 Roberts, 2015, 11. Dotto & Company.
- ↑ Иэн Стюарт. Укрощение бесконечности: История математики от первых чисел до теории хаоса / пер. с англ. Е. Погосян. — М. : Манн, Иванов и Фербер, 2019. — С. 297. — ISBN 9785001174554.
- ↑ Такой перевод названия гипотезы встречается в научно-популярной литературе[33]; в научной русскоязычной литературе термин moonshine зачастую используется без перевода.
- ↑ Alexander Masters. 32 Atlas // Simon: The Genius in My Basement. — HarperCollins, 2011. — ISBN 9780007445264.
- ↑ 1 2 John Horton Conway obituary. The Times (29 апреля 2020). Дата обращения: 5 мая 2020. Архивировано из оригинала 29 апреля 2020 года.
- ↑ Larissa Queen. Mathematics Genealogy Project. — «Some Relations between Finite Groups, Lie Groups and Modular Functions». Дата обращения: 14 апреля 2020. Архивировано 9 августа 2018 года.
- ↑ 1 2 3 4 5 Roberts, 2015, 12. Truth Beauty, Beauty Truth.
- ↑ Professorships. Princeton University. Дата обращения: 24 апреля 2023. Архивировано 5 апреля 2023 года.
- ↑ 1 2 3 4 5 6 7 Roberts, 2015, 14. Optional Probability Fields.
- ↑ Siobhan Roberts. Travels With John Conway, in 258 Septillion Dimensions. The New York Times (16 мая 2020). Дата обращения: 11 марта 2023. Архивировано 11 марта 2023 года.
- ↑ 1 2 Catherine Zandonella. Mathematician John Horton Conway, a ‘magical genius’ known for inventing the ‘Game of Life,’ dies at age 82. Princeton University (14 апреля 2020). Дата обращения: 14 апреля 2020. Архивировано 15 апреля 2020 года.
- ↑ Roberts, 2015, 17. Humpty Dumpty's Prerogative.
- ↑ Mathcampers in Action! Canada/USA Mathcamp. Архивировано из оригинала 3 февраля 2001 года.
- ↑ Roberts, 2015, 16. Take It As Axiomatic.
- ↑ Janet Beery and Carol Mead. Who's That Mathematician? Paul R. Halmos Collection - Page 59. MAA (2012). Дата обращения: 26 октября 2024. Архивировано 5 апреля 2019 года.
- ↑ 1 2 Roberts, 2015, Epilogue.
- ↑ Kevin Hartnett. John Conway Solved Mathematical Problems With His Bare Hands. Quanta Magazine (20 апреля 2020). Дата обращения: 20 апреля 2020. Архивировано 20 апреля 2020 года.
- ↑ 1 2 3 4 5 6 7 Roberts, 2015, Prologue.
- ↑ Roberts, 2015, 7. Religion.
- ↑ 1 2 Roberts, 2015, 15. Lustration.
- ↑ Ronan, 2006, p. 155.
- ↑ Wilson, 2009, 5.4 The Leech lattice and the Conway group.
- ↑ Wilson, 2009, 5.9.3 The Rudvalis group.
- ↑ Wilson, 2009, 5.7.3 Conway’s description of Fi22.
- ↑ 1 2 Ronan, 2006, 17 Moonshine.
- ↑ Terry Gannon. 0 Introduction: glimpses of the theory beneath Monstrous Moonshine // Moonshine Beyond the Monster. — Cambridge University Press, 2006. — ISBN 978-0-511-24514-5. — ISBN 978-0-521-83531-2.
- ↑ Thompson, 1984, pp. 123—127.
- ↑ William P. Thurston. Chapter 13. Orbifolds // The Geometry and Topology of Three-Manifolds : [арх. 18 октября 2023].
- ↑ Edmund Harriss, Doris Schattschneider, and Marjorie Senechal. Chapter 3. Tilings // Discrete and Computational Geometry / Ed. by Jacob E. Goodman, Joseph O'Rourke, and Csaba D. Tóth. — 3rd edition. — CRC Press, 2017. — ISBN 9781315119601.
- ↑ Michael P. Tuite. Monstrous Moonshine from orbifolds // Communications in Mathematical Physics. — 1992. — Vol. 146. — P. 277—309. — doi:10.1007/BF02102629.
- ↑ George W. Hart. Conway Notation for Polyhedra. Virtual Polyhedra (1998). Дата обращения: 3 марта 2019. Архивировано 29 ноября 2014 года.
- ↑ ATLAS of Finite Group Representations. Дата обращения: 18 октября 2023. Архивировано 18 мая 2023 года.
- ↑ Adamatzky, 2010.
- ↑ Bastien Chopard, Michel Droz. Cellular Automata Modeling of Physical Systems. — Cambridge University Press, 2005. — ISBN 9780521673457.
- ↑ Andreas Deutsch, Sabine Dormann. Cellular Automaton Modeling of Biological Pattern Formation. — Springer Science & Business Media, 2007. — ISBN 9780817644154.
- ↑ Designing Beauty: The Art of Cellular Automata / A. Adamatzky, G. J. Martínez (Eds.). — Springer International Publishing, 2016. — (Emergence, Complexity and Computation ; vol. 20). — ISBN 978-3-319-27270-2. — ISBN 978-3-319-27269-6.
- ↑ Michael M. Skolnick, David L. Spooner. Graphical User Interface in Introductory Computer Science : [арх. 9 августа 2021] // NECC '95, Baltimore, MD. — 1995. — P. 279—285.
- ↑ Robert Bosch and Julia Olivieri. Game-of-Life Mosaics : [арх. 27 марта 2019] // Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture. — 2014. — P. 325—328.
- ↑ Weisstein, Eric W. Paterson's Worms (англ.) на сайте Wolfram MathWorld.
- ↑ Weisstein, Eric W. Collatz Problem (англ.) на сайте Wolfram MathWorld.
- ↑ Alexander J. Hahn. Quadratic Forms over ℤ from Diophantus to the 290 Theorem : [арх. 17 мая 2019] // Advances in Applied Clifford Algebras. — 2008. — Vol. 18. — P. 665—676. — doi:10.1007/s00006-008-0090-y.
- ↑ Slavik V. Jablan and Radmila Sazdanovic. From Conway Notation to LinKnot // Knot Theory and Its Applications / ed. by Krishnendu Gongopadhyay and Rama Mishra. — AMS, 2016. — ISBN 978-1-4704-2257-8. — ISBN 978-1-4704-3526-4.
- ↑ J. Hoste. The enumeration and classification of knots and links // Handbook of Knot Theory / ed. by William Menasco and Morwen Thistlethwaite. — Elsevier, 2005. — P. 220. — ISBN 9780080459547.
- ↑ M. Epple. Geometric aspects in the development of knot theory // History of Topology / ed. by I. M. James. — Elsevier, 1999. — P. 309. — ISBN 9780080534077.
- ↑ Erica Klarreich. Graduate Student Solves Decades-Old Conway Knot Problem. Quanta Magazine (19 мая 2020). Дата обращения: 3 июня 2023. Архивировано 17 апреля 2021 года.
- ↑ 1 2 Roberts, 2015, 13. Mortality Flash.
- ↑ F. Scardigli. Introduction // Determinism and Free Will / Fabio Scardigli, Gerard 't Hooft, Emanuele Severino, Piero Coda. — Springer, 2019. — P. 10. — ISBN 9783030055059.
- ↑ Richard K. Guy, Tanya Khovanova, Julian Salazar. Conway's subprime Fibonacci sequences // Mathematics Magazine. — 2014. — Vol. 87. — P. 323—337. — arXiv:1207.5099. — doi:10.4169/math.mag.87.5.323.
- ↑ Richard K. Guy. John Horton Conway: Mathematical Magus // The Two-Year College Mathematics Journal. — 1982. — Vol. 13, no. 5. — P. 290—299. — doi:10.2307/3026500.
- ↑ T. Bolognesi. Spacetime Computing: Towards Algorithmic Causal Sets with Special-Relativistic Properties // Advances in Unconventional Computing: Volume 1: Theory / ed. by Andrew Adamatzky. — Springer, 2016. — P. 272—273. — ISBN 9783319339245.
- ↑ Джон Хортон Конвей (англ.) в проекте «Математическая генеалогия»
- ↑ Mathematical Gates (Faulkes Gatehouse). Isaac Newton Institute for Mathematical Sciences. Дата обращения: 17 февраля 2022. Архивировано 13 июня 2021 года.
- ↑ 1 2 List of LMS prize winners. London Mathematical Society. Дата обращения: 15 февраля 2019. Архивировано 30 сентября 2019 года.
- ↑ John Conway. Royal Society. Дата обращения: 15 февраля 2019. Архивировано 21 марта 2019 года.
- ↑ John Horton Conway. American Academy of Arts and Sciences. Дата обращения: 16 апреля 2020. Архивировано 12 апреля 2020 года.
- ↑ Past Winners: Nemmers Prize. Northwestern University. Дата обращения: 16 февраля 2024. Архивировано 2 декабря 2023 года.
- ↑ 2000 Steele Prizes (англ.). American Mathematical Society. Дата обращения: 9 августа 2013. Архивировано 21 января 2022 года.
- ↑ Joseph Priestley Award. Дата обращения: 15 марта 2019. Архивировано 21 апреля 2019 года.
- ↑ Reviews § Genius at Play: The Curious Mind of John Horton Conway, by Siobhan Roberts. AMS. Дата обращения: 17 февраля 2022. Архивировано 3 февраля 2020 года.
- ↑ John Horton Conway. Bibliography. Princeton University Department of Mathematics. — Список книг не совсем верен. Дата обращения: 6 марта 2019. Архивировано 17 мая 2019 года.
Литература
[править | править код]О Конвее
[править | править код]- Siobhan Roberts. Genius At Play. The Curious Mind of John Horton Conway. — Bloomsbury USA, 2015. — Errata. — ISBN 9781620405932.
- Siobhan Roberts. A Life in Games. Quanta Magazine (28 августа 2015). Дата обращения: 4 июня 2020. Перевод: Джон Хортон Конвей: Жизнь, как игра.
Математическая литература
[править | править код]- Человек, который играл в математику. Сборник памяти Джона Конвея / пер. с англ. Б. Р. Френкина. — МЦНМО, 2023. — ISBN 978-5-4439-1787-0.
- Thomas M. Thompson. From Error-Correcting Codes through Sphere Packings to Simple Groups. — MAA, 1984.
- Mark Ronan. Symmetry and the Monster. — Oxford University Press, 2006. — ISBN 9780192807229.
- Robert A. Wilson. The Finite Simple Groups. — Springer, 2009. — Addenda and corrigenda. — ISBN 978-1-84800-987-5. — ISBN 978-1-84800-988-2.
- Aaron A. Siegel. Combinatorial Game Theory. — AMS, 2013. — ISBN 9780821851906.
- Andrew Adamatzky. Game of Life Cellular Automata. — Springer-Verlag London, 2010. — ISBN 978-1-84996-216-2. — ISBN 978-1-84996-217-9.
Эта статья входит в число избранных статей русскоязычного раздела Википедии. |
- Родившиеся 26 декабря
- Родившиеся в 1937 году
- Родившиеся в Ливерпуле
- Умершие 11 апреля
- Умершие в 2020 году
- Умершие в Нью-Брансуике (Нью-Джерси)
- Преподаватели Принстонского университета
- Учёные Кембриджского университета
- Выпускники Кембриджского университета
- Члены Лондонского королевского общества
- Лауреаты премии Пойи (Лондонское математическое общество)
- Лауреаты премии Бервика
- Лауреаты премии Стила за математическое изложение
- Персоналии по алфавиту
- Учёные по алфавиту
- Джон Конвей
- Математики Великобритании
- Математики США
- Выпускники колледжа Гонвилл-энд-Киз
- Преподаватели Математического факультета Принстонского университета
- Почётные доктора Ясского университета
- Почётные доктора Ливерпульского университета
- Умершие от COVID-19 в США





